Digitization, occupancy, etc


Previous: 4 Small rectangles: LDRD   |   Index   |   Next: Digitization for the pixels



1) In order to cast the MC data in the form of the 'raw data' we need to asign each hit cluster to a particular silicon detector wafer. Using the local and global coordinates of the Pisa hit, we can find the location of the silicon detector center.
diagram


This is the result for layer 12. -------------------------------->
Same for layer 10 type 1 (tilted DOE)
Same for layer 9 type 1 (tilted DOE)
Same for layer 10 type 2 (flat DOE)
The angles can be cleanly digitized (1-48) and a cut on radius separated inner / outer silicon (1-2). The local x coordinate separates the left from the right half of the silicon, for a total of 192 'packets'.
The energy deposition (from Pisa) is partitioned among the strips that are hit. Here is the distribution for tracks that are approximately normally incident on 300 micron silicon. MPV is 22000 e, and the mean is 24000 e.
The code uses the first event to automatically recognize which of the four detector types (DOE cones or flat, LDRD tilted or straight) is simulated in the input file ancsvx_softlink.root, and digitize accordingly. Besides different geometry, there is also differing silicon thickness, affecting the digitization.
Here is the digitized 8-chip module number distribution for the last layer, if you use an LDRD input file - there are 20 such modules in the simulation.
The code produces a new ntuple that looks more like raw data, and allows us to study 2-track separations.

Current version of digi_all.C 

 
          hit[12] = int_ang;            // angle index of silicon panel
	  hit[13] = int_r;              // radius index of si panel
	  for (ii=0; ii<=10; ii++) {    // loop over hit cluster
            hit[14+ii] = nstrip[ii];    // silicon strip number
            hit[25+ii] = estrip[ii];    // # electrons in the signal
          }
The following plots look at a single column of ministrips in the first plane ('layer 9') of the DOE detector (type 1 = cone, type 2 = flat), using central gold-gold events, with the event vertex at z=0.
This is the part of the detector where occupancies are the highest.

(files /phenix/data07/hubert/pythia2/ auau/ancsvx_auau_typeX.root, where X is 1-4)

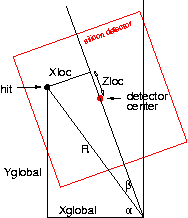
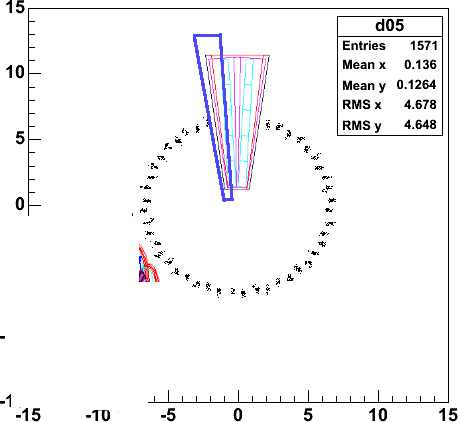
I look at the smallest readout unit, a single column of ministrips, serviced by 5 readout chips (outlined in dark blue in the figure).

The plots are for these configurations: type 1 is the lampshades, type 2 is the flat planes
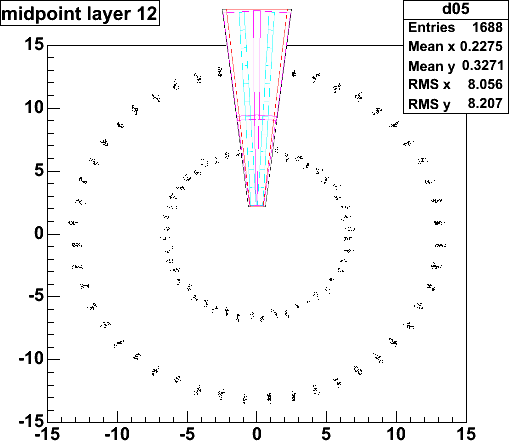
Track distribution vs strip number. The inner silicon is 6.6 cm high, so that there are 880 75-um strips. There is a small difference between the two configurations due to the plane's angles.
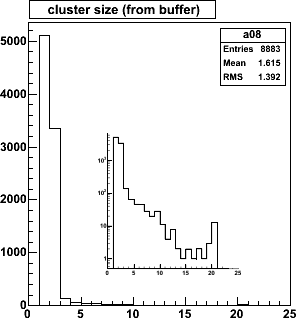
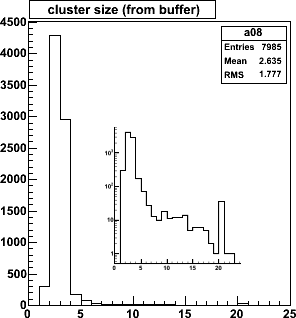
Hits are clustered because of the track angles and the detector tilt. Cluster sizes average 1.6 and 2.6, but there is a tail to large cluster sizes, as shown in the inset (same plot, log scale). The cutoff at 20 is an artfact - my internal buffer size.
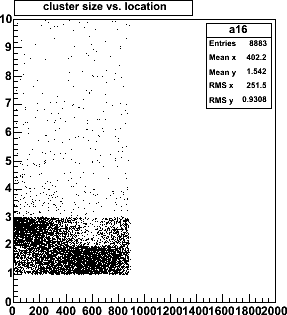
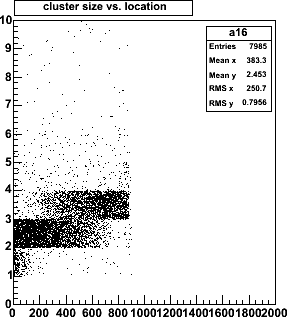
The cluster size depends on the hit location. This is most easily seen for the flat configuration (right), where there are clusters of size 1 at the innermost strips, and clusters of size 3 further out at channel 880, 6.6cm further out.

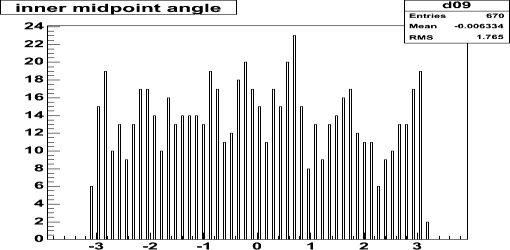
The left plot shows that tracks come in perpendicularly around strip number 600, where 1-strip clusters are most prevalent, and 2-strip clusters are more likely ar higher and at lower strip numbers.

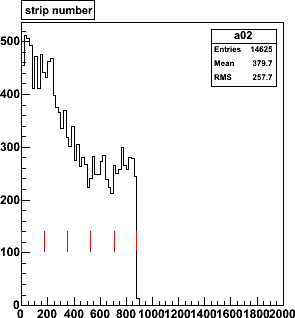
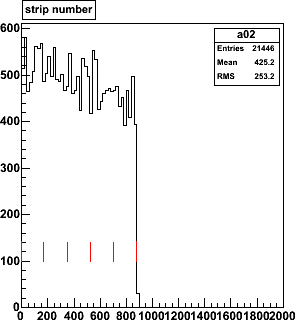
Folding the track distribution with the cluster size distribution leads to strip hit distribution, shown here for 9 AuAu events. For the flat planes, the falling track density os compensated by the increasing cluster size.

On the left, you can see the dip at strip 600, where tracks are perpendicular.

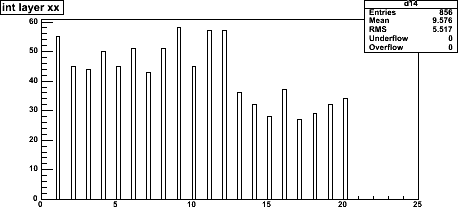
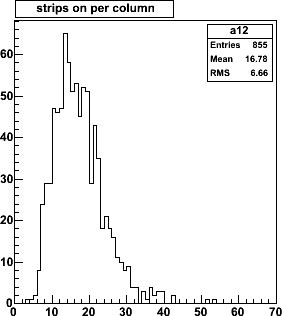
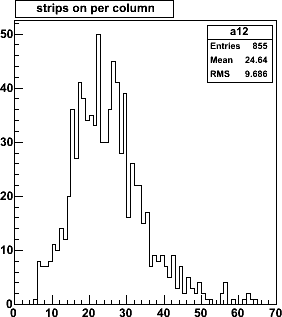
Number of strip hits per column of ministrips for 9 events (96 columns × 9 = 855 entries). Mean occupancies are 1.8% and 2.8%.
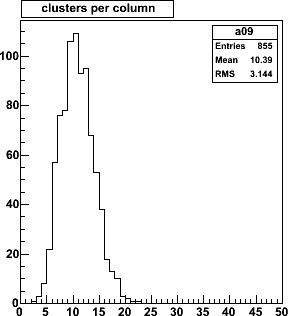
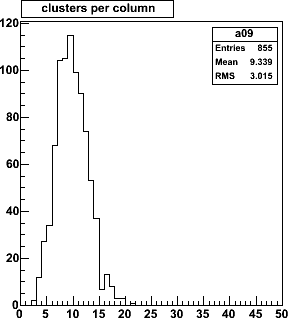
This is the distribution of clusters per ministrip column. Typically there are 10 clusters distributed over 880 strips, which is a 1.1% cluster density (~= track density).

Typically there are 1000 tracks (10.44× 96) hitting the first cone in a central AuAu event.

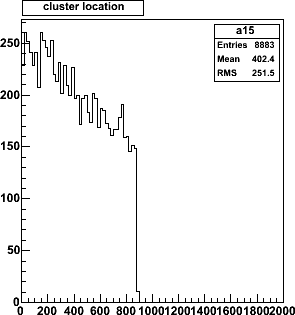
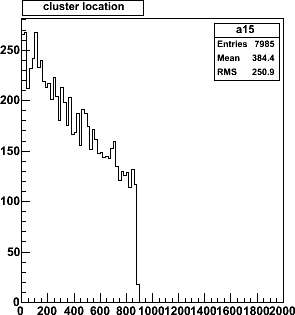
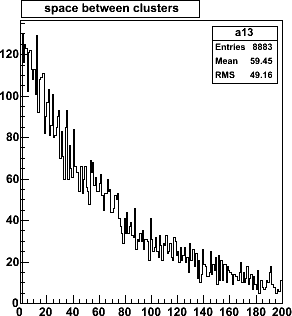
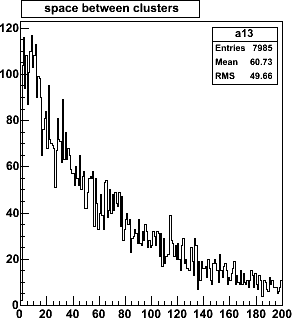
Distribution of empty space (counted in strips) between adjacent clusters. An (extrapolated) separation of 0 strips means we have merging or overlapping clusters. The probability of such merging clusters is 125/8883, or 110/7985 = 1.4%, the same for both configurations.

The pattern recognition will have to deal with these (rare) overlap occurrences.

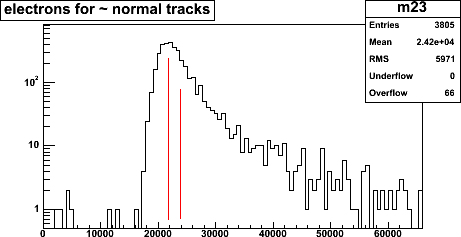
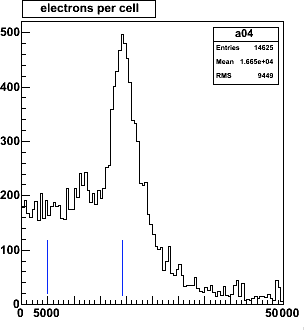
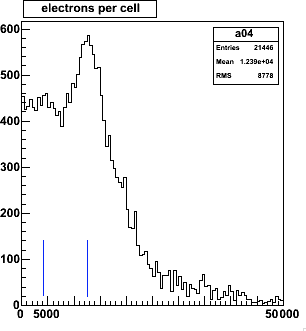
Electrons per strip hit, 17k and 12k respectively. A threshold cut is indicated, at 1/4 of the most probable value: ~5000 and 4000 electrons, respectively.
Same plots for 50 um strips

Writeup of this in in MSWord format or as a ppt presentation


Previous: 4 Small rectangles: LDRD   |   Index   |   Next: Digitization for the pixels