Digitization


1) In order to cast the MC data in the form of the 'raw data' we need to asign each hit cluster to a particular silicon detector wafer. Using the local and global coordinates of the Pisa hit, we can find the location of the silicon detector center.
diagram


This is the result for layer 12. -------------------------------->
Same for layer 10 type 1 (tilted DOE)
Same for layer 9 type 1 (tilted DOE)
Same for layer 10 type 2 (flat DOE)
The angles can be cleanly digitized (1-48) and a cut on radius separated inner / outer silicon (1-2). The local x coordinate separates the left from the right half of the silicon, for a total of 192 'packets'.
The energy deposition (from Pisa) is partitioned among the strips that are hit. Here is the distribution for tracks that are approximately normally incident on 300 micron silicon. MPV is 22000 e, and the mean is 24000 e.
The code uses the first event to automatically recognize which of the four detector types (DOE cones or flat, LDRD tilted or straight) is simulated in the input file ancsvx_softlink.root, and digitize accordingly. Besides different geometry, there is also differing silicon thickness, affecting the digitization.
Here is the digitized 8-chip module number distribution for the last layer, if you use an LDRD input file - there are 20 such modules in the simulation.
The code produces a new ntuple that looks more like raw data, and allows us to study 2-track separations.

Current version of digi_all.C 

 
          hit[12] = int_ang;            // angle index of silicon panel
	  hit[13] = int_r;              // radius index of si panel
	  for (ii=0; ii<=10; ii++) {    // loop over hit cluster
            hit[14+ii] = nstrip[ii];    // silicon strip number
            hit[25+ii] = estrip[ii];    // # electrons in the signal
          }
The following plots look at a single column of strips in the first plane ('layer 9') of the cone DOE detector ('type 1'), using central gold-gold events, with the event vertex at z=0.
This is the part of the detector where occupancies are the highest.

(files /phenix/data07/hubert/pythia2/ auau/ancsvx_auau_typeX.root, where X is 1-4)

I look at the smallest readout unit, a single column of ministrips, serviced by 5 readout chips (outlined in dark blue in the figure).

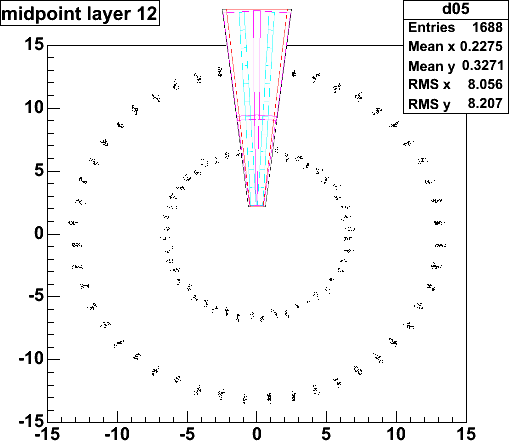
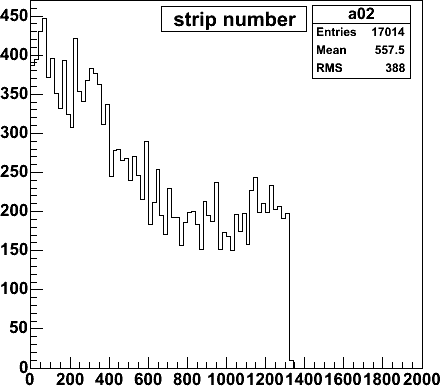
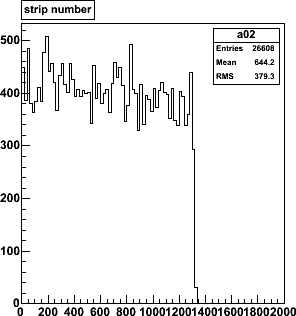
This is the strip hit distribution for 9 AuAu events. The inner silicon is 6.6 cm high, so that there are 1320 50-um strips. The hit distribution is not flat, due to the non-uniform angular distribution of tracks in the AuAu events.

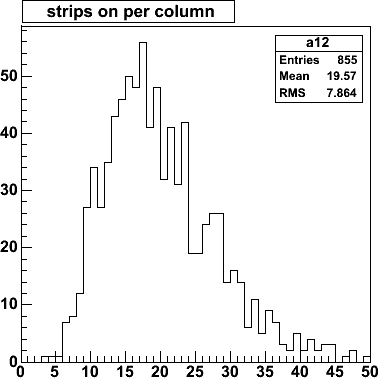
Hits per column of strips for 9 events (96 columns × 9 = 855 entries). 20/1320= 1.5% occupancy.
Hits are clustered because of the track angles and the detector tilt. Cluster sizes average 1.9, but there is a tail to large cluster sizes, as shown in the inset (same plot, log scale). The cutoff at 20 is an artfact - my internal buffer size.
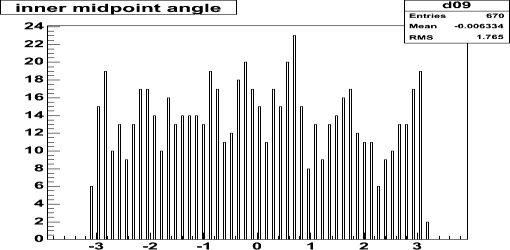
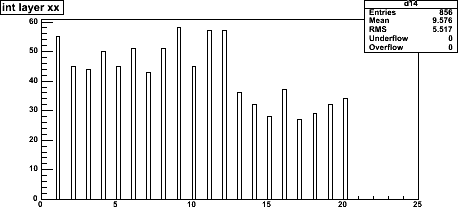
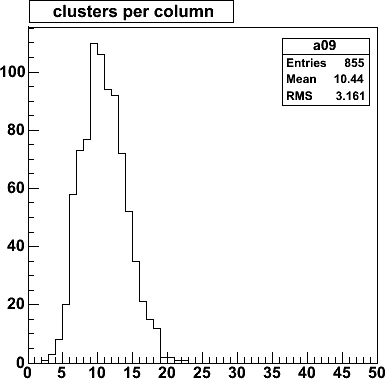
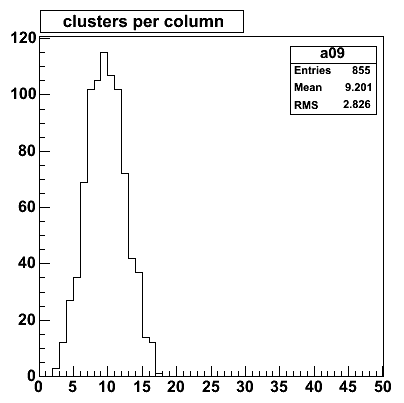
This is the distribution of clusters per column. Typically there are 10 clusters distributed over 1320 strips, which is a 0.76% cluster density (~= track density).

Typically there are 1000 tracks (10.44× 96) hitting the first cone in a central AuAu event.

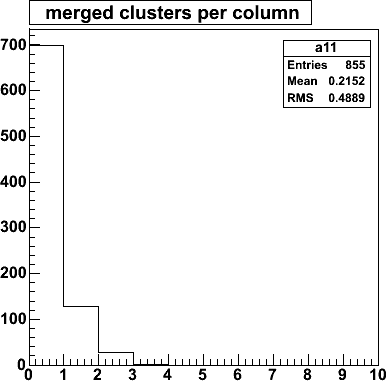
Number of overlapping clusters per column. Since the mean number of clusters per 1320-strip column is 10, the mean distance between clusters is 132 strips. With the cluster size ~2, this means that most of these mergers are not random overlaps. See this column printout
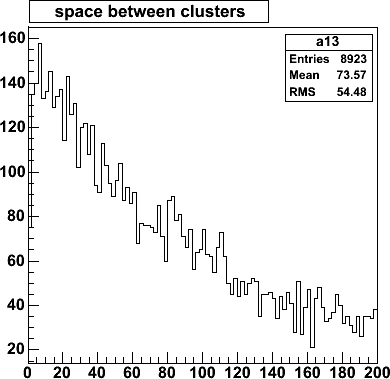
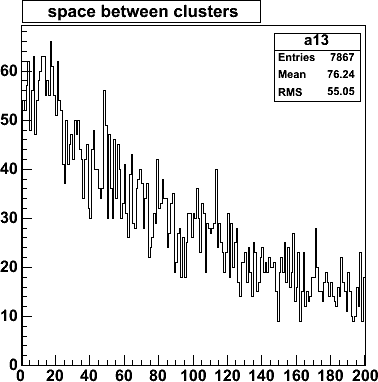
Distribution of empty space between clusters
Number of overlapping clusters per column. Since the mean number of clusters per 1320-strip column is 10, the mean distance between clusters is 132 strips. With the cluster size ~2, this means that most of these mergers are not random overlaps.
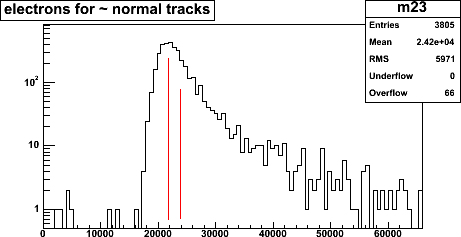
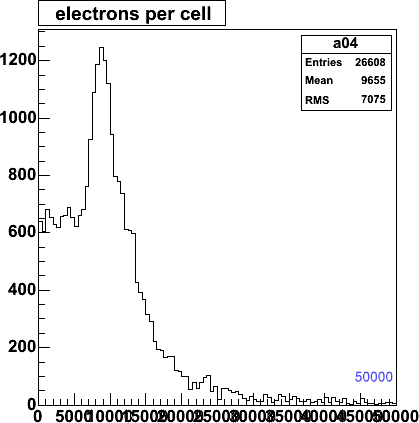
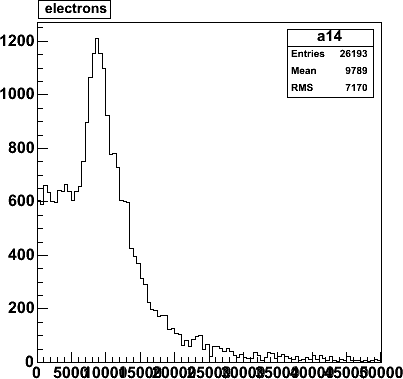
Electrons per hit