



Next: Transversity Measurements in
Up: Spin Physics with
Previous: Spin Physics with
The Drell-Yan (DY) process[17], 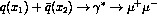 (or
(or 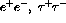 ), has been studied for over twenty years,
largely by measuring muon pairs in fixed target experiments at Fermilab and
CERN[18]. With the advent of QCD descriptions, including next-to-leading-order
corrections, it can be characterized as well understood theoretically[18].
Phenomenological evaluations of parton structure functions now routinely use DY as well
as DIS data. The parton-model expression for the DY cross section,
), has been studied for over twenty years,
largely by measuring muon pairs in fixed target experiments at Fermilab and
CERN[18]. With the advent of QCD descriptions, including next-to-leading-order
corrections, it can be characterized as well understood theoretically[18].
Phenomenological evaluations of parton structure functions now routinely use DY as well
as DIS data. The parton-model expression for the DY cross section,
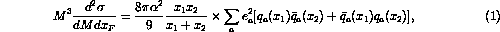
is often multiplied by a factor,  , which accounts for next-to-leading order
QCD effects.
, which accounts for next-to-leading order
QCD effects.
We first consider the measurement of 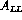 in the DY process, since its close relation
to
in the DY process, since its close relation
to 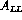 of DIS experiments allows a reasonably quantitative analysis.
The expression for the
longitudinal spin asymmetry in the DY process has the simple form[8,14],
of DIS experiments allows a reasonably quantitative analysis.
The expression for the
longitudinal spin asymmetry in the DY process has the simple form[8,14],
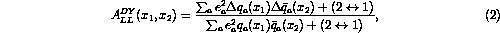
with 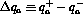 . The superscripts refer to parton spin projections parallel (+) or
antiparallel (-) to the parent hadron's spin projection. For
. The superscripts refer to parton spin projections parallel (+) or
antiparallel (-) to the parent hadron's spin projection. For
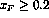 the denominator of Eq. 2 is dominated by the term,
the denominator of Eq. 2 is dominated by the term,
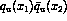 , allowing a substantial
simplification,
, allowing a substantial
simplification,
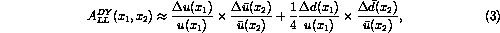
where the notation 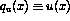 has been introduced.
Neglecting small sea-quark effects, one can use approximate expressions for the structure
functions of DIS,
has been introduced.
Neglecting small sea-quark effects, one can use approximate expressions for the structure
functions of DIS,
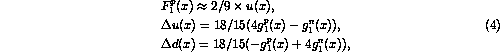
to achieve an important further simplification.
The measured values of
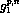 in DIS are shown in Figs 4 and 5. For
in DIS are shown in Figs 4 and 5. For 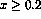 one sees that
one sees that
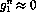 , and with the above relations Eq. 3 becomes,
, and with the above relations Eq. 3 becomes,
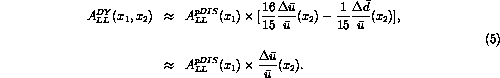
The second step follows if 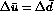 . Equation 5 has
the familiar form of an experimentally measured asymmetry being determined by the product of a beam
polarization and the asymmetry of a physical process. Thus for the DY process with
. Equation 5 has
the familiar form of an experimentally measured asymmetry being determined by the product of a beam
polarization and the asymmetry of a physical process. Thus for the DY process with 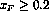 , a longitudinally polarized proton can be thought of as a beam of polarized u quarks with
, a longitudinally polarized proton can be thought of as a beam of polarized u quarks with
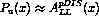 . It is apparent from the large measured values of
. It is apparent from the large measured values of
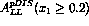 that longitudinal spin asymmetry in the DY process
will be a sensitive measure of the polarization of the
that longitudinal spin asymmetry in the DY process
will be a sensitive measure of the polarization of the  quark distribution of
the proton.
quark distribution of
the proton.
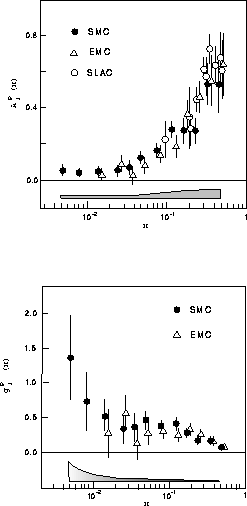
Figure 4: Longitudinal asymmetry and 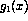 structure function for
deep-inelastic lepton scattering from the proton from
CERN[1,4] and SLAC[2]
structure function for
deep-inelastic lepton scattering from the proton from
CERN[1,4] and SLAC[2]
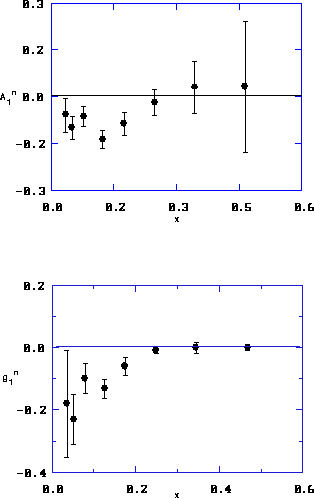
Figure 5: Longitudinal asymmetry and 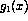 structure function for
deep-inelastic lepton scattering from the neutron (
structure function for
deep-inelastic lepton scattering from the neutron ( ) from
SLAC[6]
) from
SLAC[6]
Equation 5 permits estimates to be made for actual experimental conditions,
given some assumptions about the antiquark polarization. Until recently little guidance
could be found on the subject of antiquark polarization beyond the strong indication that
the strange quark sea makes a significant integral contribution to the proton's
spin[3,4,5]. Bourrely and Soffer[19] adopt an approach to
quark and antiquark polarization inspired by a possible connection between light-flavor
asymmetries and spin asymmetries. Two recent experiments[20,21]
strongly suggest
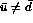 in the proton. Bourrely and Soffer propose,
in the proton. Bourrely and Soffer propose,
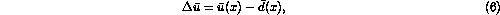
where the relation is fixed at 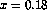 by a recent measurement of the
by a recent measurement of the 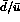 asymmetry of the proton using the DY process[21].
asymmetry of the proton using the DY process[21].
Equations 1 (including a K-factor of 2) and 5 can be used with the model of
Ref.[19] to make sensitivity estimates for realistic running conditions. Monte Carlo DY
events are thrown in to the full acceptance of the enhanced PHENIX muon spectrometer, with
100% detection efficiency assumed for single muons above 2 GeV in the end caps, and above 1.3 GeV
in the central arms. The luminosity of RHIC is assumed[16] to be
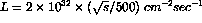 . Results at
. Results at 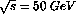 for
an integrated luminosity
for
an integrated luminosity
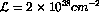 are shown in Fig. 6; beam polarizations were taken to be
0.7[16]. A total of 10.8 K muon pairs,
are shown in Fig. 6; beam polarizations were taken to be
0.7[16]. A total of 10.8 K muon pairs, 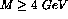 , are detected (Table 1). The errors
on
, are detected (Table 1). The errors
on 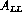 would be twice as large if measured at
would be twice as large if measured at 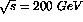 with an integrated
luminosity
with an integrated
luminosity 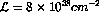 (see Appendix B). With the proposed PHENIX muon upgrade
a sensitive measurement of the antiquark helicity distribution of the proton is clearly feasible.
(see Appendix B). With the proposed PHENIX muon upgrade
a sensitive measurement of the antiquark helicity distribution of the proton is clearly feasible.
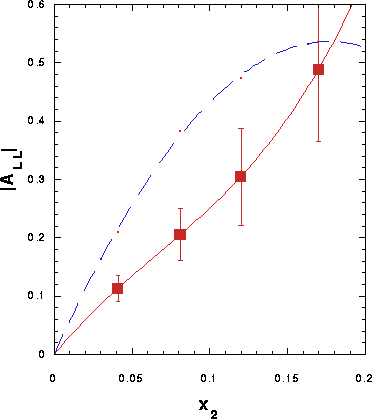
Figure 6: 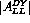 using Eq. 5 and the model of Bourrely
and Soffer[19]. Two extrapolations consistent with
the experimental results from CERN NA51[21] yield the
two curves. Error bars (shown on the lower curve) are based on an
integrated luminosity of
using Eq. 5 and the model of Bourrely
and Soffer[19]. Two extrapolations consistent with
the experimental results from CERN NA51[21] yield the
two curves. Error bars (shown on the lower curve) are based on an
integrated luminosity of 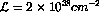 at
at 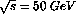 , yielding
10.8K muon pairs; beam polarizations are taken to be 0.7.
, yielding
10.8K muon pairs; beam polarizations are taken to be 0.7.
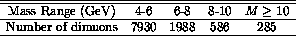
Table 1: Number of Drell-Yan dimuons detected by the upgraded
PHENIX muon spectrometer at
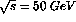 with an integrated luminosity
with an integrated luminosity 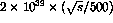 .
.
Based on extensive experience with dimuon production in fixed-target experiments, the most
serious source of background competing with the DY process is semileptonic charm decay. Drell-Yan
production experiments at Fermilab[23,24] (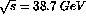 ) provide strong
evidence that the charm contribution is negligible for
) provide strong
evidence that the charm contribution is negligible for 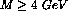 . However extensive
simulations performed for the PHENIX CDR[25] indicate competition from charm
decay for
. However extensive
simulations performed for the PHENIX CDR[25] indicate competition from charm
decay for
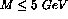 at
at
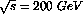 where the production cross section is considerably larger.
where the production cross section is considerably larger. Thus relatively low energies
for DY physics are also indicated from the standpoint of background minimization.
Thus relatively low energies
for DY physics are also indicated from the standpoint of background minimization.




Next: Transversity Measurements in
Up: Spin Physics with
Previous: Spin Physics with
Converted to HTML from LaTeX by W. Wayne Kinnison
Sun Nov 5 18:47:30 MST 1995
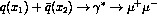 (or
(or 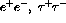 ), has been studied for over twenty years,
largely by measuring muon pairs in fixed target experiments at Fermilab and
CERN[18]. With the advent of QCD descriptions, including next-to-leading-order
corrections, it can be characterized as well understood theoretically[18].
Phenomenological evaluations of parton structure functions now routinely use DY as well
as DIS data. The parton-model expression for the DY cross section,
), has been studied for over twenty years,
largely by measuring muon pairs in fixed target experiments at Fermilab and
CERN[18]. With the advent of QCD descriptions, including next-to-leading-order
corrections, it can be characterized as well understood theoretically[18].
Phenomenological evaluations of parton structure functions now routinely use DY as well
as DIS data. The parton-model expression for the DY cross section,
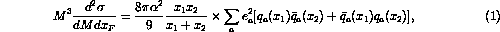
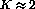 , which accounts for next-to-leading order
QCD effects.
, which accounts for next-to-leading order
QCD effects.
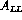 in the DY process, since its close relation
to
in the DY process, since its close relation
to 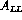 of DIS experiments allows a reasonably quantitative analysis.
The expression for the
longitudinal spin asymmetry in the DY process has the simple form[
of DIS experiments allows a reasonably quantitative analysis.
The expression for the
longitudinal spin asymmetry in the DY process has the simple form[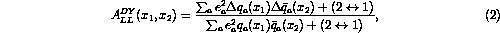
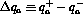 . The superscripts refer to parton spin projections parallel (+) or
antiparallel (-) to the parent hadron's spin projection. For
. The superscripts refer to parton spin projections parallel (+) or
antiparallel (-) to the parent hadron's spin projection. For
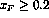 the denominator of Eq.
the denominator of Eq. 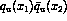 , allowing a substantial
simplification,
, allowing a substantial
simplification,
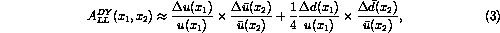
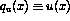 has been introduced.
Neglecting small sea-quark effects, one can use approximate expressions for the structure
functions of DIS,
has been introduced.
Neglecting small sea-quark effects, one can use approximate expressions for the structure
functions of DIS,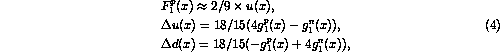
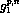 in DIS are shown in Figs
in DIS are shown in Figs 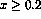 one sees that
one sees that
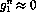 , and with the above relations Eq.
, and with the above relations Eq. 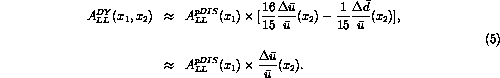
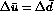 . Equation
. Equation 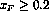 , a longitudinally polarized proton can be thought of as a beam of polarized u quarks with
, a longitudinally polarized proton can be thought of as a beam of polarized u quarks with
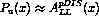 . It is apparent from the large measured values of
. It is apparent from the large measured values of
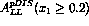 that longitudinal spin asymmetry in the DY process
will be a sensitive measure of the polarization of the
that longitudinal spin asymmetry in the DY process
will be a sensitive measure of the polarization of the  quark distribution of
the proton.
quark distribution of
the proton.

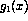 structure function for
deep-inelastic lepton scattering from the proton from
CERN[
structure function for
deep-inelastic lepton scattering from the proton from
CERN[
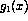 structure function for
deep-inelastic lepton scattering from the neutron (
structure function for
deep-inelastic lepton scattering from the neutron ( ) from
SLAC[
) from
SLAC[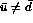 in the proton. Bourrely and Soffer propose,
in the proton. Bourrely and Soffer propose,
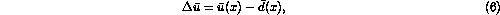
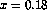 by a recent measurement of the
by a recent measurement of the 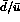 asymmetry of the proton using the DY process[
asymmetry of the proton using the DY process[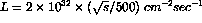 . Results at
. Results at 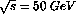 for
an integrated luminosity
for
an integrated luminosity
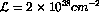 are shown in Fig.
are shown in Fig. 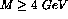 , are detected (Table
, are detected (Table 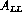 would be twice as large if measured at
would be twice as large if measured at 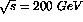 with an integrated
luminosity
with an integrated
luminosity 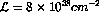 (see Appendix B). With the proposed PHENIX muon upgrade
a sensitive measurement of the antiquark helicity distribution of the proton is clearly feasible.
(see Appendix B). With the proposed PHENIX muon upgrade
a sensitive measurement of the antiquark helicity distribution of the proton is clearly feasible.

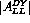 using Eq.
using Eq. 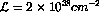 at
at 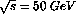 , yielding
10.8K muon pairs; beam polarizations are taken to be 0.7.
, yielding
10.8K muon pairs; beam polarizations are taken to be 0.7.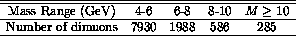
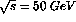 with an integrated luminosity
with an integrated luminosity 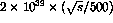 .
.
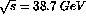 ) provide strong
evidence that the charm contribution is negligible for
) provide strong
evidence that the charm contribution is negligible for 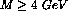 . However extensive
simulations performed for the PHENIX CDR[
. However extensive
simulations performed for the PHENIX CDR[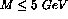 at
at
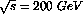 where the production cross section is considerably larger.
where the production cross section is considerably larger.