vertex at 0, vertex RMS = 0 cm	vertex at 1 cm, vertex RMS = 0 cm	vertex mean at 0, RMS = 5 cm
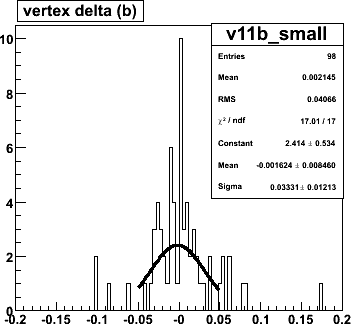
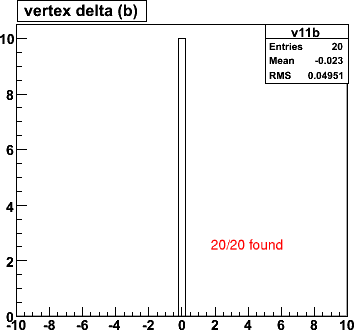
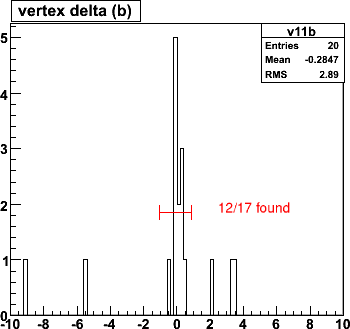
Throw some 5-GeV muons into the North arm. Case 1: vertex at 0, case 2: vertex at +1cm. In the third column, the event vertex is spread with pisa command DIAMOND 0 0 0 0 0 5.0 This gives a 5 cm RMS z-spread. (Note there are 3 over/underflows).
For each event, pick a trial vertex z-position. From there, plot tan(theta) for all hits in all stations. If there is an entry in a tan(theta)-bin, it is likely to be the only entry in the bin, if the trial z is not the event z, and if the binning is fine enough. If the trial vertex z is the same as the real vertex z, hits in the 4 planes will tend to line up, and entries per bin should be closer to 4. 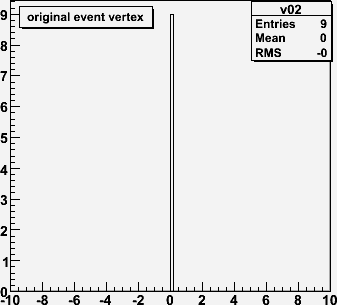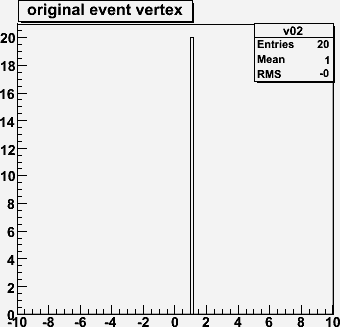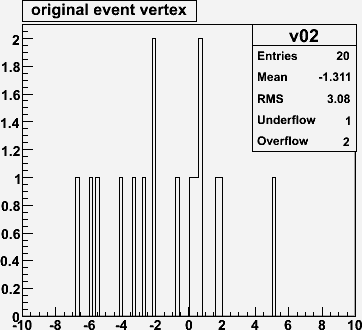For non-empty bins, calculate the mean number of entries. It will be a little more than 1.0.
Scanning between z=-10 and +10 cm, this is the mean of the non-zero entris
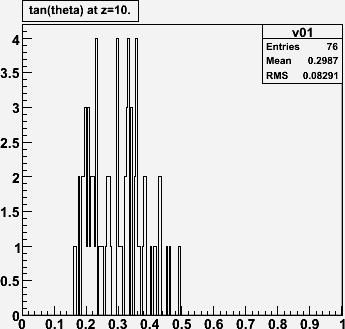
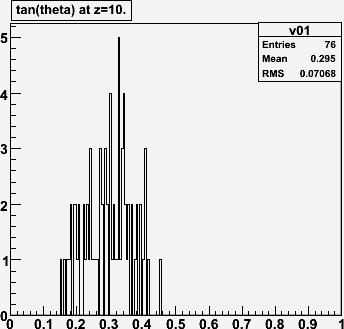
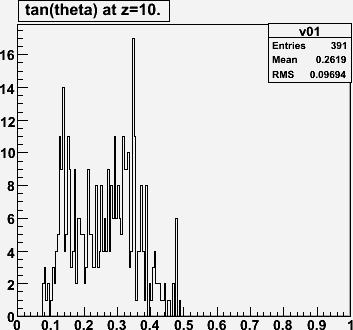
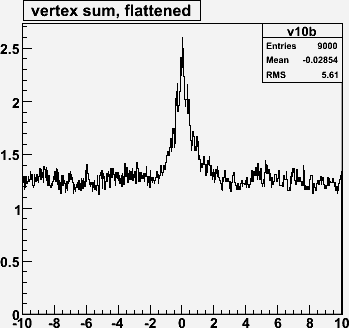
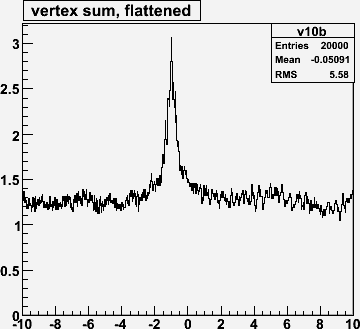
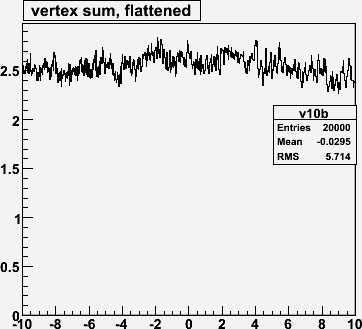
Difference between the real vertex and the reconstructed vertex, by finding the highest bin in the histo above. In the third case, only 12 out of 17 vertices are found correctly. (to be continued...)

[Clearly there is trouble in the 3rd column, where vertices are spread widely. Needs to be debugged - could be a multiplicity problem]

Files:
vertex.C

To be done:

• The method is multiplicity-dependent. Busier events require finer binning. This needs to be automatically detected
• Study the optimum resolution of the method
• Transport code into offline code (this is ancsvx-level code).
• Recognize and flag when the event vertex is not found. Currently some z-value is always produced.