Next: Electronics Requirements
Up: The Vertex Detector For
Previous: Vertex from the
We have assumed that the vertex needs to be known to better than 1mm in z. In
the plane transverse to the beam, the definition is already equal to the beam
size (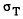
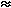 0.45mm for Au+Au5,9). Some chip placement
aberrations result in a track ending up in a strip neighboring the expected
one, reducing the peak value of the correlation function. Preventing this kind
of error defines most of the constraints on placement of the chips in 3
directions, z (along the beam axis), R (radial), and s (circumferential, or
R*d
0.45mm for Au+Au5,9). Some chip placement
aberrations result in a track ending up in a strip neighboring the expected
one, reducing the peak value of the correlation function. Preventing this kind
of error defines most of the constraints on placement of the chips in 3
directions, z (along the beam axis), R (radial), and s (circumferential, or
R*d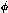 ), plus the 3 rotations around these axes. The chips lie at radii
R1 and R2, which are assumed to be 6 and 9 cm in the calculations below.
The size of a chip in the z-direction (Zchip) is taken to be 5cm, and the
detector "cylinders" have a hexagonal cross-section.
), plus the 3 rotations around these axes. The chips lie at radii
R1 and R2, which are assumed to be 6 and 9 cm in the calculations below.
The size of a chip in the z-direction (Zchip) is taken to be 5cm, and the
detector "cylinders" have a hexagonal cross-section.
The correlation method is only concerned with the relative placement of
chip pairs, one chip on the inner cylinder and the corresponding chip(s) on the
outer cylinder. Here, one example of the determination of the alignment
constraints is given. The other constraints are determined similarly and are
summarized in table 5.
Consider the displacement in R (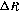 ) of one of the cylinders
relative to the other. When scaling the outer pattern by the nominal
R1/R2, a radial displacement would result in a pattern that is
improperly scaled. A calibration procedure could find the actual R1/R2,
but the nominal ratio will presumably be a ratio of integers, hard-wired in a
fast vertex finder. In order to limit the error such that in the worst case, a
track is displaced by 1 strip (100
) of one of the cylinders
relative to the other. When scaling the outer pattern by the nominal
R1/R2, a radial displacement would result in a pattern that is
improperly scaled. A calibration procedure could find the actual R1/R2,
but the nominal ratio will presumably be a ratio of integers, hard-wired in a
fast vertex finder. In order to limit the error such that in the worst case, a
track is displaced by 1 strip (100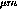 ),
),
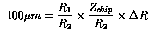 (2)
(2)
This is satisfied if radial displacement of the outer chip is less than
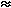 0.3mm.
0.3mm.
| axis | max. error in relative position | max. error for relative rotation about this axis |
|---|
| z (beam) | 0.5mm | 0.15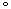 |
| R (transverse) | 0.3mm | 0.1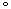 |
| s (circumference) | 0.5mm | 0.3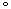 |
Table 5: Summary of tolerances in placement of inner/outer chip pairs
relative to each other from correlation method
These tolerances, summarized in table 5, are between inner/outer chip pairs
only. Suppose that a chip pair is joined such that they meet these tolerances.
There are further constraints on the positions of chips pairs relative to the
beam. Again, consider one example. There is a constraint in R, which leads to a
limit of:
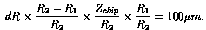 (3)
(3)
The pair must be placed at a radial distance which is known better than
dR 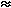 0.8mm. This should be compared to the size of the Au+Au beam in the
transverse direction5,9,
0.8mm. This should be compared to the size of the Au+Au beam in the
transverse direction5,9, 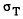
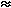 0.45mm. Table 6 summarizes
the constraints on the positions of pairs of chips relative to the beam. These
constraints are not as stringent as those on the relative positions of the
chips.
0.45mm. Table 6 summarizes
the constraints on the positions of pairs of chips relative to the beam. These
constraints are not as stringent as those on the relative positions of the
chips.
| axis | max. error | max. error for rotation about this axis |
|---|
| z | 5.0mm | 1 |
| R | 0.8mm | 37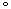 |
| s | 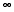 | 4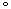 |
Table 6: Summary of tolerances on the placement of chip pairs relative to the
beam from correlation method, where each pair of chips are positioned relative
to each other within the tolerances given in table 5.
The correlation method of vertex finding leads to the limits given in
tables 5 and 6. The pseudo-tracking method combines a hit on any of the inside
chips with a hit on any of the outer chips, which may pose limits on the
relative placement of all chips simultaneously, not just in pairs. In order for
this method to work, all pairs must be able to point to the same vertex. This
implies relative placement requirements between any pairs of chips similar to
those in table 5. However, this is an offline method, and the positions of
chips may be calibrated using tracks reconstructed from other detectors. Such
calibrations would work for all aberrations except rotations around r and z.
However the tolerances imposed on these angular placements by the correlation
method are much more stringent than anything needed to define a vertex to 1mm.
Thus the pseudo-tracking method imposes no further restrictions.



Next: Electronics Requirements
Up: The Vertex Detector For
Previous: Vertex from the
Converted to HTML by:
Christine Jarmer
Mon Jun 24 08:52:44 MDT 1996
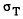
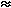 0.45mm for Au+Au5,9). Some chip placement
aberrations result in a track ending up in a strip neighboring the expected
one, reducing the peak value of the correlation function. Preventing this kind
of error defines most of the constraints on placement of the chips in 3
directions, z (along the beam axis), R (radial), and s (circumferential, or
R*d
0.45mm for Au+Au5,9). Some chip placement
aberrations result in a track ending up in a strip neighboring the expected
one, reducing the peak value of the correlation function. Preventing this kind
of error defines most of the constraints on placement of the chips in 3
directions, z (along the beam axis), R (radial), and s (circumferential, or
R*d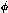 ), plus the 3 rotations around these axes. The chips lie at radii
R1 and R2, which are assumed to be 6 and 9 cm in the calculations below.
The size of a chip in the z-direction (Zchip) is taken to be 5cm, and the
detector "cylinders" have a hexagonal cross-section.
), plus the 3 rotations around these axes. The chips lie at radii
R1 and R2, which are assumed to be 6 and 9 cm in the calculations below.
The size of a chip in the z-direction (Zchip) is taken to be 5cm, and the
detector "cylinders" have a hexagonal cross-section.
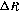 ) of one of the cylinders
relative to the other. When scaling the outer pattern by the nominal
R1/R2, a radial displacement would result in a pattern that is
improperly scaled. A calibration procedure could find the actual R1/R2,
but the nominal ratio will presumably be a ratio of integers, hard-wired in a
fast vertex finder. In order to limit the error such that in the worst case, a
track is displaced by 1 strip (100
) of one of the cylinders
relative to the other. When scaling the outer pattern by the nominal
R1/R2, a radial displacement would result in a pattern that is
improperly scaled. A calibration procedure could find the actual R1/R2,
but the nominal ratio will presumably be a ratio of integers, hard-wired in a
fast vertex finder. In order to limit the error such that in the worst case, a
track is displaced by 1 strip (100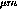 ),
),
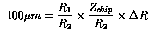 (2)
(2)
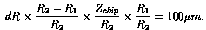 (3)
(3)