Phenix Note 125-CSC Design

NEXT:Prototype Measurements UP:Introduction

2. Cathode Strip Readout Chamber Design Issues

The primary design issues addressed have been factors effecting the intrinsic resolution of the chambers, the mechanical and electronic requirements, and the definition of a suitable gas. Where possible we have relied on the work of previous authors and in particular the vast amount of work done by the Muon Group and the Central Tracker Group of the former GEM collaboration at the SSC.

2.1 CSCR Candidate Gases

It is desirable to have a gas with a small Lorentz angle so resolution degradation due to a large Lorentz angle can be minimized. Fortunately, a number of fast gases have been identified and tested that are suitable for the CSCR's[2],[3]. Most of these gases contain CF_4 in combination with isobutane or C0_2. The Lorentz angle is similar for each gas and is about 5 degrees at 0.5 Tesla magnetic field. Most of the prototype work has been done with a 50% CF_4, 50% isobutane mixture but C0_2 is also an acceptable replacement for the isobutane.

2.2 Resolution Degradation due to Inclined Tracks and the Lorentz Angle

Resolution degradation of the CSRC's comes primarily from two causes, tracks inclined from the normal to the face of the chamber and Lorentz angle. In both cases the position resolution is degraded because the deposited charge is distributed nonuniformly along the anode wire due to the energy loss fluctuations in the gas. These effects have been extensively studied by the former Muon Group in the GEM collaboration and reported in a GEM note (V. A. Polychronakos and V. Tcherniatine, GEM TN-92-137, July 1992). Additional studies by Musser et al. in GEM-93-408 for the GEM Central Tracker Group on a CSRC type chamber very similar to the proposed PHENIX CSRC's and for a suitable gas (50% CO_2,50% CF_4) have shown that the resolution degradation, d, is equal to

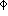
	d = .08 d tan

where d is the cathode to cathode spacing and 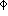is the angle from the normal to the face of the chamber. Including Lorentz angle smearing, , is accomplished by modifying the angle of incidence by the Lorentz angle, i.e. 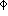-. In Figures 2.2.1 and 2.2.2, we show the chamber resolutions when these effects are taken into account. The Lorentz angle was taken to be 5 degrees. In Figure 2.2.1 the resolution is plotted for chambers with different intrinsic resolutions and the chamber gap = 6 mm. In Figure 2.2.2 the resolution is plotted for different chamber gaps with the resolutions fixed at 100 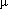m. It is clear that we want thin chambers and small angles of incidence and resolutions approaching 100 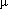m. Since it might be preferable to support the anode wire every meter because of electrostatic considerations, the anode wires could be placed with a support that bisects the chamber octant. This support would be very similar in design to that proposed in GEM TN-92-137 and shown in Figure 2.2.3. We have not optimized this for the CSRC but expect a similar improvement in performance.

Figure 2.2.1: Resolution degradation with angle for different intrinsic resolutions

Figure 2.2.2: Resolution for different chamber gaps at 100 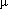m intrinsic resolution

2.3 Mechanical Design Issues

The mechanical issues associated with CSRC are addressed more fully in a separate document. In summary, finite element calculations have been performed on the frame and frame support structure to understand distortions due to the wire and foil loads. The support frame is shown in Figure 2.3.1 and results are shown in Figure 2.3.2. The support frame is fabricated from graphite composite material to provide stiffness and to keep the normal modes above 40 Hz. The deflections are small and do not pose a problem either in maintaining adequate tension on the anode wires or in assuring that the foils remain stretched. Since the z thickness of the station 2 is less than 7.5 cm, adjacent frames can be overlapped as shown below, thereby minimizing acceptance losses.

A technique to etch the thin kapton foil has been developed that allows the etching process to be done on the foil after the foil has been stretched on the support frame. This process involves electroetching the gold coated kapton with a probe tip attached to a low voltage source. The tip is mounted on a computer controlled x-y table and positioned with an accuracy of 10 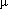m by a linear slide. A drawing of this setup is shown in Figure 2.3.3. Since the kapton foil is available in widths up to only l.5 meters, station 2 and 3 must have foils that are glued together to get the required dimensions. A technique for gluing kapton foil was used successfully on cylindrical chambers for the MEGA experiment at LAMPF[4]. They have not experienced any problems in 3 years. We expect to adapt that technique to the CSRC foils. Tests are now underway. Creep of kapton foils occurs in the first few days after stretching. Experience with 1-meter stretched kapton foils at LAMPF has shown no unacceptable loss in foil tension over 4 years. Generally, the foil will not sag under gravity load until the foil tension has almost fully relaxed. Our experience has shown this relaxation appears not to be a problem.

Figure 2.2.3: GEM Muon chamber design

Figure 2.3.1: Support frame for CSRC showing graphite composite

Figure 2.3.2: Results of finite element analysis of CSRC frame

Figure 2.3.3: Setup for etching stretched cathode foils on frames

2.4 Electronic Design Issues

The primary design issue for the front-end electronics is to maintain a signal-to-noise of better than 100/1 in the face of a large detector capacitance. For the CSRC chambers the dominant contribution to the capacitance seen by the preamplifiers is the strip-to-strip capacitance. The capacitance between adjacent strips having a thickness, t, width, w, and separation, s, laying on a dielectric with constant, k, is approximately given by,

	C(pf/cm) = 0.12t/w + O.O9(1+k)1og_10(l + 2w/s + w^2/s^2).

The second term dominates. Using k=3.5 (kapton), w=10 mm, s = 0.5 mm, t = 2 microns, the capacitance is 1.1 pf/cm. For the prototype test chamber the capacitance was measured to be 1.33 pf/cm in close agreement to the calculated value. We expect the maximum capacitance will be less than 500 pf for all stations so a basic requirement of the front-end electronics is that it must perform to specifications with an input capacitance of 500 pf or less.

Figure 2.4.1: SPICE simulations of cathode strip

An additional concern is the coupling of the signals between adjacent strips. A test of this effect was modeled in the electronic code PSPICE for representative chamber parameters. For this simulation the strips were considered as lumped RC delay lines. The results of the simulation are shown in Figure 2.4.1. A current pulse similar to signals observed on the prototype chamber was injected into one end of the simulated cathode strip and the pulse response was observed at the far end of the active strip as well as the adjacent strip. The total interstrip capacitance was 300 pf, the resistance was 20 ohms, and the capacitance to the anode plane was 10 pf. The results show significant coupling to the adjacent strip and dispersion of the initial signal. However, if the signal is integrated for > 100 ns the full signal charge is preserved and the signal on the adjacent strip integrates to zero. This implies that the integration time of the electronics should be greater than 100 ns if we want to be insensitive to any distortions in the apparent induced charge distribution due to coupling from one strip to another.

NEXT:Prototype Measurements UP:Introduction