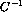 and
and
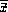 . The other set of output data was then used
for calculating the DF.
. The other set of output data was then used
for calculating the DF.
In order to test the discrimination power of the DF one set of
PISA output data
at each energy was used for calculating the values of 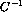 and
and
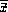 . The other set of output data was then used
for calculating the DF.
. The other set of output data was then used
for calculating the DF.
We find that the DF produces very good discrimination between muons and pions of known equal (or sufficiently close) momenta. However, the results depend on the ``bias'' that is chosen. For a large negative bias, all pions are correctly identified but all muons are incorrectly identified as pions. For large positive bias the reverse is true. As the bias is varied from negative to positive values around zero, the fraction of correctly identified muons increases and the fraction of correctly identified pions decreases. We present our results in a format that shows this variation with changing bias. The results of the Discriminant Analysis for the three schemes shown in Fig. 2 are summarized in Figs. 3, 4, and 5.
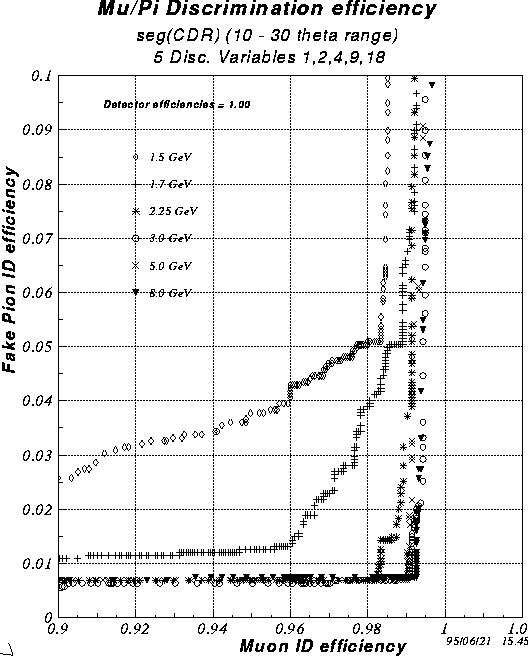
Figure 3: Discrimination efficiency for pad layout described in
the PHENIX CDR (Case 1 in Fig. 2).
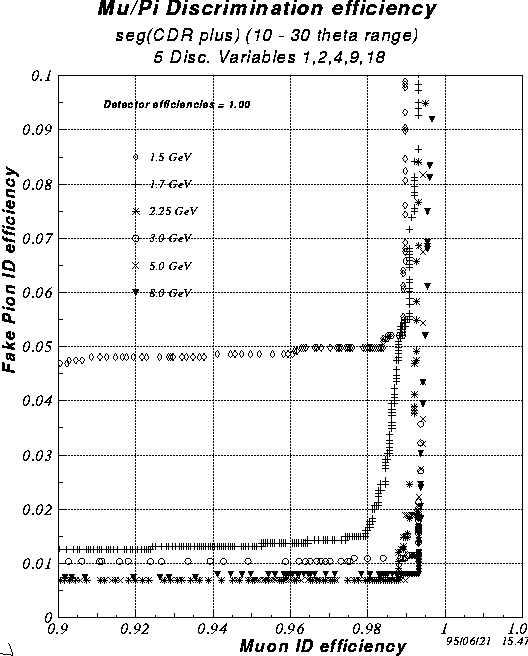
Figure 4: Discrimination efficiency for pad layout
shown for Case 2 in Fig. 2.
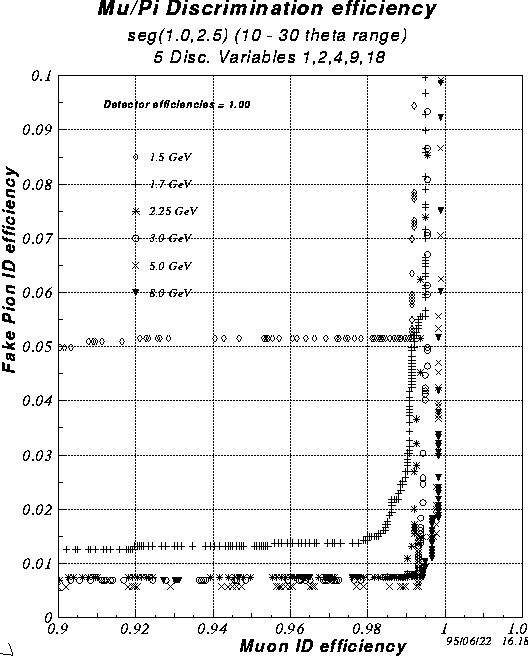
Figure 5: Discrimination efficiency for pad layout
shown for Case 3 in Fig. 2.
Each of these shows plots of the fraction of muon tracks correctly identified as muons (``Muon ID efficiency'') versus the fraction of pion tracks incorrectly identified as muons (``Fake Pion ID efficiency''). In all cases five discriminant variables were used:
 between the beam axis
and the straight-line fit to the road.
between the beam axis
and the straight-line fit to the road.
This set of discriminant variables is not exactly the same as used by Saskia Mioduszewski [3] but the results are very insensitive to the choice of variables. Roughly speaking, any three or four variables are sufficient and the use of more than four or five does not improve the discrimination power.
As indicated in the figures, the discrimination power is nearly perfect for
all the incident particle momenta above 2.25 GeV/c. The abrupt degradation
in performance below that momentum can be explained on the basis of the
fact that, at about
this momentum, some of the muons are not able to completely
penetrate all six layers of the muon identifier. At 1.5 GeV/c none of the
muons reaches beyond plane 5. At momenta for which the muons are able to
penetrate all
six layers, muons and pions are easily distinguished from each
other.
At these momenta there is no need to closely match the momentum of the
particles used to produce the training data
with the momentum of the test particles. For example,
the results for 5 GeV/c are
equally good if either 3 GeV/c or 8 GeV/c training data are used
for calculating 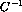 and
and 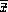 .
.