


Next: Discriminant Analysis Results
Up: Discriminant Analysis
Previous: Discriminant Analysis
The technique of Discriminant Analysis [1],[2]
is one of the methods we have used
for discriminating between muons and
pions. To perform this analysis one creates in an ad hoc
fashion a set of variables that are functions of the hit
patterns
in the detector pads.
These variables are chosen to hopefully produce
different values
depending on whether they are produced by a pion track or a muon track.
This method can be thought of as treating each variable as the
axis of a P-dimensional space, where P is the number of variables used.
A particle event is then described as a point or vector with P components
in this space. A series of events of one type (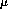 ) will form a cluster of
points in this space while events of another type (
) will form a cluster of
points in this space while events of another type ( ) will
hopefully form a
separate cluster. These clusters can be separated by a hyper-surface lying
between them. It can be shown [2]
that for variables with a Gaussian distribution the best such surface is
described by the discriminant function DF with DF = 0 where
) will
hopefully form a
separate cluster. These clusters can be separated by a hyper-surface lying
between them. It can be shown [2]
that for variables with a Gaussian distribution the best such surface is
described by the discriminant function DF with DF = 0 where
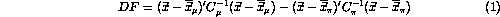
where the  are the values of the P-dimensional vectors and the
are the values of the P-dimensional vectors and the
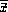 are their average values. The quantities
are their average values. The quantities 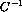 are elements of the inverse of the covariance matrix given by
are elements of the inverse of the covariance matrix given by
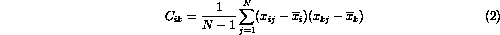
where 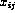 is parameter-i from event j.
is parameter-i from event j.
The magnitudes
of the diagonal elements 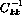 are large if the distribution of the
parameters they represent
are very narrow. However, their significance is obscured by the fact that
their
magnitudes are also directly proportional to the average values
are large if the distribution of the
parameters they represent
are very narrow. However, their significance is obscured by the fact that
their
magnitudes are also directly proportional to the average values
 .
Therefore it is helpful to normalize the averages to some convenient value.
The values of DF are unaffected if Eqs. 1 and 2 are
replaced by
.
Therefore it is helpful to normalize the averages to some convenient value.
The values of DF are unaffected if Eqs. 1 and 2 are
replaced by
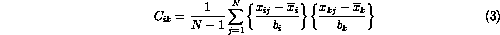
and
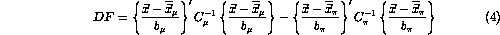
It is important to note that the values of DF are unaffected by the choice
of 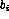 . Equation 1 simply uses
. Equation 1 simply uses 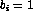 . Two other ways of
determining
. Two other ways of
determining 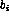 that are
particularly useful are
that are
particularly useful are
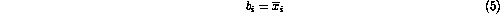
which has the effect of normalizing the mean values of all the parameters to
unity. The
``sharpness'' of parameter k is then proportional to the magnitude of the
diagonal element 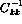 .
Of course the value of a given parameter in discriminating between the two
types of
particles also depends on the value of
.
Of course the value of a given parameter in discriminating between the two
types of
particles also depends on the value of 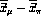 . If this
difference is close to zero the parameter will be of no value and may, in
fact, produce
poorer discrimination than if it is not used at all.
. If this
difference is close to zero the parameter will be of no value and may, in
fact, produce
poorer discrimination than if it is not used at all.
Applied to the present data, if the clusters of parameter values for
muon (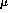 ) and pion (
) and pion ( ) events are well separated we will have
) events are well separated we will have
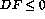 for muons and
for muons and 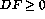 for pions. In practice, the
clusters are not completely separated and some of each type of particle
will be mis-identified. It
is frequently desirable to choose some value
for pions. In practice, the
clusters are not completely separated and some of each type of particle
will be mis-identified. It
is frequently desirable to choose some value 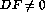 to produce
an acceptable combination of pion rejection and muon acceptance. We will
refer to the value of DF used to achieve a particular combination of
pion rejection and muon acceptance as the ``bias''.
to produce
an acceptable combination of pion rejection and muon acceptance. We will
refer to the value of DF used to achieve a particular combination of
pion rejection and muon acceptance as the ``bias''.



Next: Discriminant Analysis Results
Up: Discriminant Analysis
Previous: Discriminant Analysis
Converted to HTML from LaTeX by Christine Jarmer
Thu Nov 9 08:58:12 MST 1995
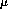 ) will form a cluster of
points in this space while events of another type (
) will form a cluster of
points in this space while events of another type ( ) will
hopefully form a
separate cluster. These clusters can be separated by a hyper-surface lying
between them. It can be shown [2]
that for variables with a Gaussian distribution the best such surface is
described by the discriminant function DF with DF = 0 where
) will
hopefully form a
separate cluster. These clusters can be separated by a hyper-surface lying
between them. It can be shown [2]
that for variables with a Gaussian distribution the best such surface is
described by the discriminant function DF with DF = 0 where
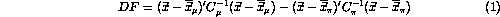
 are the values of the P-dimensional vectors and the
are the values of the P-dimensional vectors and the
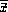 are their average values. The quantities
are their average values. The quantities 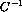 are elements of the inverse of the covariance matrix given by
are elements of the inverse of the covariance matrix given by
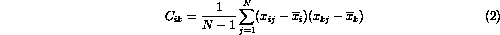
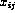 is parameter-i from event j.
is parameter-i from event j.
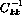 are large if the distribution of the
parameters they represent
are very narrow. However, their significance is obscured by the fact that
their
magnitudes are also directly proportional to the average values
are large if the distribution of the
parameters they represent
are very narrow. However, their significance is obscured by the fact that
their
magnitudes are also directly proportional to the average values
 .
Therefore it is helpful to normalize the averages to some convenient value.
The values of DF are unaffected if Eqs.
.
Therefore it is helpful to normalize the averages to some convenient value.
The values of DF are unaffected if Eqs. 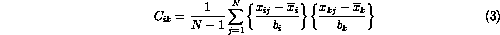
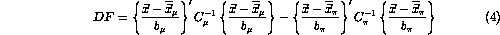
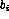 . Equation 1 simply uses
. Equation 1 simply uses 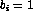 . Two other ways of
determining
. Two other ways of
determining 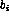 that are
particularly useful are
that are
particularly useful are
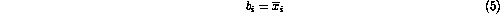
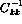 .
Of course the value of a given parameter in discriminating between the two
types of
particles also depends on the value of
.
Of course the value of a given parameter in discriminating between the two
types of
particles also depends on the value of 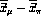 . If this
difference is close to zero the parameter will be of no value and may, in
fact, produce
poorer discrimination than if it is not used at all.
. If this
difference is close to zero the parameter will be of no value and may, in
fact, produce
poorer discrimination than if it is not used at all.
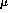 ) and pion (
) and pion ( ) events are well separated we will have
) events are well separated we will have
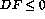 for muons and
for muons and 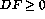 for pions. In practice, the
clusters are not completely separated and some of each type of particle
will be mis-identified. It
is frequently desirable to choose some value
for pions. In practice, the
clusters are not completely separated and some of each type of particle
will be mis-identified. It
is frequently desirable to choose some value 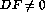 to produce
an acceptable combination of pion rejection and muon acceptance. We will
refer to the value of DF used to achieve a particular combination of
pion rejection and muon acceptance as the ``bias''.
to produce
an acceptable combination of pion rejection and muon acceptance. We will
refer to the value of DF used to achieve a particular combination of
pion rejection and muon acceptance as the ``bias''.