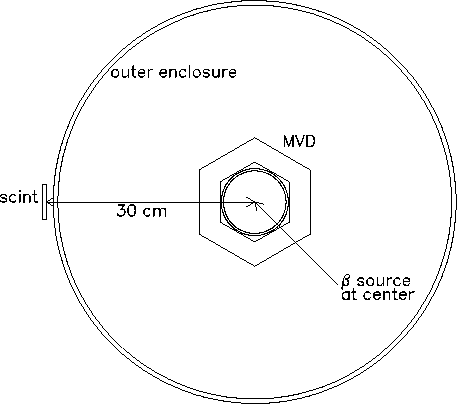
The assumed geometry is sketched below:

First, estimate the energy loss of electrons going through the MVD. The material involved in the pisa (geant based) model of the MVD is:

Particles going through the rohacell cages could completely miss the material in the cages, they could go through up to 2.5 cm of rohacell, or anything in between. The following table summarizes the amount of material in the MVD and the approximate energy loss in each material.

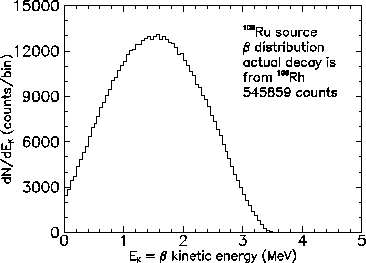
To start with, I had to create a more or less correct beta distribution. Mine is not perfect, and should slightly overestimate the counting rate because it produces too many higher energy beta's. Details are are here.

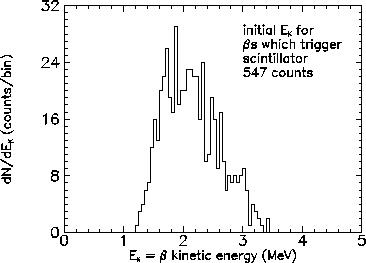
A pisa simulation of the MVD showed that a minimum energy of about 1 MeV was needed go through all of the material and then to trigger the scintillator in this model. The back of the envelope calculation above gives an estimated average energy loss of 0.4 MeV in the material. Combining this with the 0.5 MeV threshold required for the scintillator gives a cutoff of 0.9 MeV -- in reasonable agreement. For details on the pisa code used, click here.

In an effort to include material which should be in the model, but is not (e.g. glue, paralene), a calculation with the density of rohacell increased by a factor of 4 was done. This should increase the average amount of material by 315 mg/cm^2 -- more than doubling it. This should be a significant overestimate. It should increase the expected energy loss by about 0.63 MeV -- to about 1.5 MeV when the scintillator's discriminator threshold is included. A calculation showed a cutoff around 1.4 MeV -- again in reasonable agreement with expectations.

The following two plots show the initial kinetic energy distribution of a betas in the simulation followed by the initial kinetic energy distribution for those betas which triggered the scintillator. This calculation assumed rohacell had 4 times it true density (see above).

Next, I did a calculation with a source which isotropically omitted beta particles. I counted the number of these electrons which trigger the scintillator. This fraction was 547/545859. Assume that the particles which generate the trigger all go through a single Si wafer (an oversimplification, but useful for the estimates below). There are 256 Si channels per wafer. To get N_hits hits per channel in each of these channels, we would require about N_decays = 256*545859*N_hits/547 = (255466+-10922)*N_hits beta decays. If we want N_hits to be about 500 and we would like to do this in 10 minutes (for example), this defines the activity of the source needed: 255466*500 decays/600 sec = 212888+-9102 decays/sec. A micro-Curie is 3.7E4 decays/sec, so this source strength would be 212888/3.7E4 = 5.75+-.25 microCurie .

In an earlier estimate for the strength of a gamma source, I had estimated that we would need about 2.65Curie -- about 460K times larger. This estimate had assumed that there would be no trigger at all -- so the rate would need to be high enough to get a significant hit rate in each strip of the MVD.