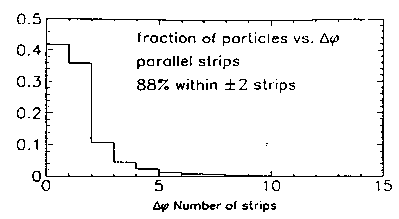
Figure 6: Probability vs. the difference in the parallel strip in the outer barrel which was hit and the strip that would have been hit with no multiple scattering. All charged particles which hit both barrels are included.
There are two stages in the pseudo-tracking vertex search. First, only the
parallel strips are used, obviating the need to test all pairs of hits as each
parallel strip covers a small 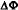 (azimuthal angle). Particles from
the central axis of the vertex detector have the same
(azimuthal angle). Particles from
the central axis of the vertex detector have the same 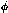 at each barrel,
except for small variations due to multiple scattering. Fig. 6 shows a
distribution of the change in the strip number hit in the outer barrel due to
multiple scattering in the inner barrel; most particles hit the outer barrel
within
at each barrel,
except for small variations due to multiple scattering. Fig. 6 shows a
distribution of the change in the strip number hit in the outer barrel due to
multiple scattering in the inner barrel; most particles hit the outer barrel
within 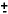 2 strips of the expected position. For each hit in the outer
barrel, all hits in the inner barrel which are within
2 strips of the expected position. For each hit in the outer
barrel, all hits in the inner barrel which are within 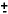 2 strips are used
to calculate a possible vertex position. The top part of fig. 7 shows the
resulting distribution of vertices for a sample Au+Au event. An estimate of the
event vertex appears as a peak. The peak height gives the number of particles
hitting both barrels of this half of the detector. The background comes from
random pairs of hits. Limiting the hits tested to
2 strips are used
to calculate a possible vertex position. The top part of fig. 7 shows the
resulting distribution of vertices for a sample Au+Au event. An estimate of the
event vertex appears as a peak. The peak height gives the number of particles
hitting both barrels of this half of the detector. The background comes from
random pairs of hits. Limiting the hits tested to 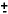 2 strips reduces the
number of pairs that must be tested by a factor of
2 strips reduces the
number of pairs that must be tested by a factor of 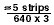 =
=
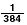 . This reduces the background in the histograms shown
in the upper half of fig. 7 by
. This reduces the background in the histograms shown
in the upper half of fig. 7 by 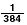 while only reducing the counts
in the peak by about 12% (see fig. 6).
while only reducing the counts
in the peak by about 12% (see fig. 6).
Figure 7: Au+Au - pseudo-tracking example. Top shows the distribution of
vertices using parallel strips only.
Bottom shows the distribution of vertices using the
perpendicular strips.
Arrows mark the true vertex and
the vertex found in each stage.
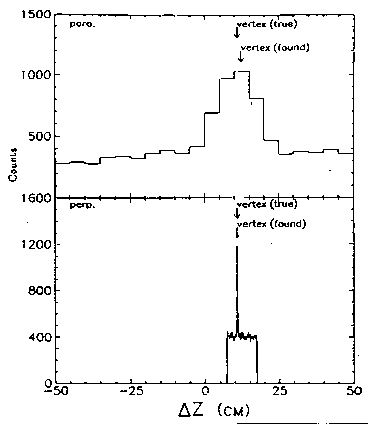
Because the peak found using pseudo-tracking with parallel strips is broad, the vertex position is estimated by taking the center of gravity of three bins around the maximum. Because the strips are long (5cm) in the z direction, this method can not give very good vertex resolution. Fig. 8 shows the vertex resolution for p+p, p+Au, and Au+Au using pseudo-tracking with parallel strips only. For p+p and p+Au, this method gives better resolution than the center of (CG) and is much less noise sensitive. However, pseudo-tracking with parallel strips alone still does not give a vertex resolution for p+p which is significantly better than the variation in the vertex position itself5.
Figure 8: The vertex resolution using pseudo-tracking with parallel strips only for p+p, p+Au minimum bias, and Au+Au central. The horizontal axis is the difference the true vertex and the vertex found.
This first stage using parallel strips is used to estimate a vertex
position. The second stage of the vertex search uses perpendicular strips which
are short in the z direction (100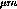 ), and determine the vertex much more
accurately. Beginning with an approximate vertex reduces the range of vertex
positions to be searched and increases the speed of the algorithm. The second
stage of the vertex search is similar to the first, but as each perpendicular
strip occupies a large
), and determine the vertex much more
accurately. Beginning with an approximate vertex reduces the range of vertex
positions to be searched and increases the speed of the algorithm. The second
stage of the vertex search is similar to the first, but as each perpendicular
strip occupies a large 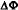 , the number of pairs of hits that must be
tested is about N1N2/3, where 3 is the number of different azimuthal
segments with perpendicular strips and N1and N2 are the number of hits
on the perpendicular strips in the inner and outer barrels, respectively. For
central Au+Au events, this number is large, so the algorithm is slow. The
vertex from the first stage of pseudo-tracking is used to restrict the pairs of
strips which are tested; for Au+Au, only those pairs of strips which point to a
vertex position within
, the number of pairs of hits that must be
tested is about N1N2/3, where 3 is the number of different azimuthal
segments with perpendicular strips and N1and N2 are the number of hits
on the perpendicular strips in the inner and outer barrels, respectively. For
central Au+Au events, this number is large, so the algorithm is slow. The
vertex from the first stage of pseudo-tracking is used to restrict the pairs of
strips which are tested; for Au+Au, only those pairs of strips which point to a
vertex position within 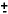 5cm of the vertex found in the first stage of
pseudo-tracking are tested. For p+p and p+Au, this range is expanded to
5cm of the vertex found in the first stage of
pseudo-tracking are tested. For p+p and p+Au, this range is expanded to 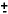 10cm. A histogram of vertex positions is calculated from the pairs of hits. An
example of one of these histograms is shown on the bottom part of fig. 7. The
vertex position appears as the peak in this distribution.
10cm. A histogram of vertex positions is calculated from the pairs of hits. An
example of one of these histograms is shown on the bottom part of fig. 7. The
vertex position appears as the peak in this distribution.
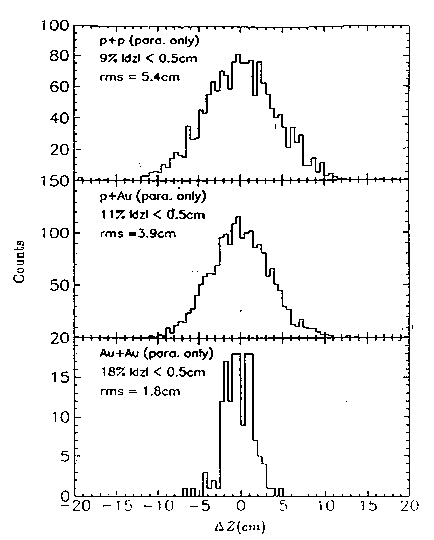
Figure 9: Notice the difference in scale from fig. 8. The vertex resolution using pseudo-tracking with both parallel and perpendicular strips for p+p, p+Au minimum bias, and Au+Au central. *Due to the bin size used, the RMS deviations are upper limits.
Fig. 9 shows the vertex resolution using both stages of pseudo-tracking. The correct vertex is found in all events tested for central Au+Au collisions. For p+p and Au+Au the correct vertex is usually found. Table 3 summarizes the efficiency of pseudo-tracking vertex search for different assumed levels of noise for the three systems. "Total events" and "triggers" are the total number of Monte Carlo events and the number of those that satisfied the "trigger" condition - at least two charged particles hitting both cylinders of the vertex detector. The column labeled "% of triggers" gives the efficiency of the vertex search algorithm - the fraction of the events for which the vertex found was within 5mm of the true vertex. The last column gives the resolution of the vertex finding algorithm based on the widths of the peaks in fig. 9. These widths are upper limits due to the size of the bins used in the pseudo-tracking algorithm. Especially for p+p collisions, noise has a significant effect on the vertex finding efficiency.
 (mm)
(mm)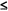 0.4
0.4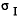 = 5.7, 16, 20cm for p+p, p+Au, Au+Au, respectively.
See text for explanation of columns.
= 5.7, 16, 20cm for p+p, p+Au, Au+Au, respectively.
See text for explanation of columns.
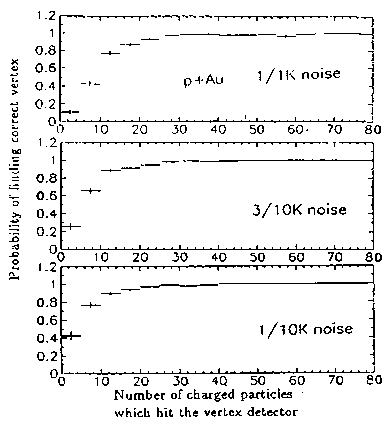
 10), but the efficiency reaches
10), but the efficiency reaches