


Next: The problem of
Up: The Vertex Detector For
Previous: Introduction and Design
The conceptual design of the vertex detector was based on two concentric,
approximately cylindrical, barrels of single-sided 300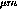 thick silicon
strips with 100
thick silicon
strips with 100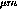 pitch2. Fig. 1 shows schematic views. Half of the
strips in each barrel are oriented parallel to z (the beam direction) and half
orthogonal to z. The parallel and perpendicular strips are sometimes called
"r-
pitch2. Fig. 1 shows schematic views. Half of the
strips in each barrel are oriented parallel to z (the beam direction) and half
orthogonal to z. The parallel and perpendicular strips are sometimes called
"r- 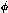 " and "z" strips, respectively.
" and "z" strips, respectively.
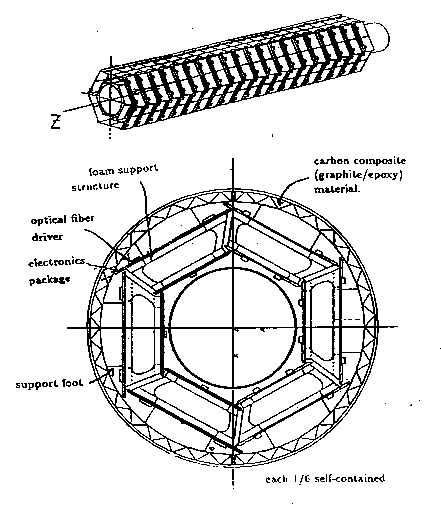
Figure 1:
The conceptual design of the vertex detector. The bottom part
shows the view along the beam line. The top part
shows a 3D perspective view.
The inner and outer
detectors should not move relative to one another;
details of these constraints are
discussed in a later section. The detector should be constructed
from "ladders" which maintain accurate relative positioning of the inner and
outer detector wafers in each azimuthal segment. Each ladder will be
constructed from Rohacell foam4, which is a very light (reduces multiple scattering) but rigid foam
whose coefficient of thermal expansion is close to that of Si. Using a
ladder-like structure, rather than a solid piece of foam, further reduces the
mass of the support structure and permits better airflow for cooling.
Based on the expected power dissipation of the chips, preamps, and
transmitters, the assembly will be air-cooled.
foam4, which is a very light (reduces multiple scattering) but rigid foam
whose coefficient of thermal expansion is close to that of Si. Using a
ladder-like structure, rather than a solid piece of foam, further reduces the
mass of the support structure and permits better airflow for cooling.
Based on the expected power dissipation of the chips, preamps, and
transmitters, the assembly will be air-cooled.
The ladders fit into a graphite/epoxy
mechanical structure with a small coefficient of thermal expansion.
The thermal expansion of the different pieces of the
detector must be considered to maintain position accuracy.
A large mismatch in the coefficients of thermal
expansion of the detector wafers and the support structure could also result in
severe damage to the detector. The modular construction of the detector
allows some azimuthal segments to be removed if necessary.
A series of simulations of the detector were performed, using a nearly
realistic model. The model was a pair of cylinders, whereas
the "real" detectors2 have a hexagonal cross-section.
The "real" detector
has dead areas around the edges of the chips, but in the simulations,
the chips are assumed to be active even at their edges. Table 1 summarizes the
number of channels assumed in the simulations of the vertex detector.
For the chips containing strips parallel to the beam, there are some
further differences between the simulations and a realistic design. The
simulations assume 150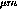 pitch for parallel strips in the outer barrel,
with 100
pitch for parallel strips in the outer barrel,
with 100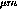 pitch in the rest of the detector. This assumption is
convenient because it means that the parallel strips in the inner and outer
barrel each occupy the same
pitch in the rest of the detector. This assumption is
convenient because it means that the parallel strips in the inner and outer
barrel each occupy the same  .
.
| barrel | strip type | R (mm) | Wafer size (mm x mm) | 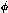 segments segments | # of wafers | strips/wafer | total strips |
|---|
| inner |  | 61.1 | 64 x 50 | 3 | 20 | 640 | 38400 |
| inner | 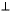 | 61.1 | 32 x 50 | 3 | 40 | 480 | 57600 |
| outer |  | 91.7 | 96 x 50 | 3 | 40 | 320 | 38400 |
| outer | 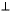 | 91.7 | 48 x 50 | 3 | 40 | 480 | 57600 |
| Totals | | | | | 140 | | 192000 |
Table 1: Summary of the number of channels in the
simulation of the vertex detector.
The shape is approximated by a cylinder, whose radius is given.
Pitch=100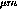 except parallel strips in the outer barrel,
where 150
except parallel strips in the outer barrel,
where 150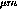 is assumed.
is assumed.
The total number of channels per barrel shown in table 1 is about
a factor of two larger than the
estimate in the introduction.
This was necessary because the distribution of particles along the
length of the detector is not uniform, and because
single particles can hit more than one strip ---
a serious problem for strips perpendicular to the beam.
The particle distributions in the simulations all come from Fritiof3.
These simulations were done for p+p, p+Au, and Au+Au collisions
assuming 100GeV/nucleon beams.
The average charged particle multiplicities from these
calculations are shown in table 2. The vertex position was assumed to always be
on the central axis of the vertex detector. The z position was varied assuming
a Gaussian distribution whose tails were cut off so that all interactions were
assumed to take place within 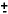 50cm of the center of the vertex detector.
The Gaussian distributions assumed5
50cm of the center of the vertex detector.
The Gaussian distributions assumed5 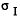 =20, 16, and 5.7cm, for
Au+Au, p+Au, and p+p collisions, respectively.
=20, 16, and 5.7cm, for
Au+Au, p+Au, and p+p collisions, respectively.
| System | <F> = fraction of particles which hit detector | <Ntotal>No. charged particles |
|---|
| Au+Au (central) | 0.64 | 5894 |
| p+Au (min-bias) | 0.55 | 50 |
| p+p | 0.56 | 21 |
Table 2: The average fraction of the particles which hit both layers of the
vertex detector and the average total number of charged particles produced.
Based on Fritiof3 for 100GeV/nucleon beams.
Each charged particle produced in the simulation was tested to see if it
would hit the vertex detector; uncharged particles were ignored. If a particle
entered the vertex detector, the program calculated which
parallel and perpendicular strips would be hit.
Multiple scattering of charged particles in the
inner barrel of the vertex detector was included. To approximately account for
the support structure and electronics, the multiple scattering
calculation assumed that the inner barrel of the vertex detector was twice its
real thickness. Particles were allowed to hit more than one
strip. When a particle hit a detector barrel,
the program calculated how much silicon a particle would pass through in
each strip of the detector.
A minimum-ionizing particle (mip) will lose an average of 116 keV in
300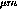 of Si. The
result of this was an array giving the amount of Si (approximately equivalent
to the energy loss) that particles passed through in a strip.
of Si. The
result of this was an array giving the amount of Si (approximately equivalent
to the energy loss) that particles passed through in a strip.
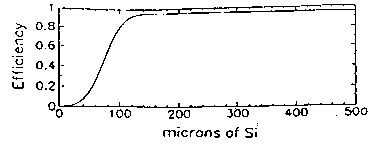
Figure 2: Assumed efficiency as a function of
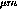 of Si traversed in a cell.
of Si traversed in a cell.
The array giving the amount of Si traversed in each strip is used to generate
a pattern of "hits" in the strips. This is done using the efficiency function
shown in fig. 2, which shows the efficiency as a function of the amount of Si
traversed in a strip. The maximum efficiency6 was assumed to be 95%. A
"threshold", corresponding to 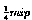 (or 75
(or 75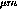 of Si here) was
assumed. A noise level, which was varied from 0.1% to 0.01%
was included in the efficiency function --- this means that a strip which was
not hit has a small probability (Pnoise) to be "on".
If a strip was "on" then each of the adjacent strips were
assumed to have a 10% probability to be "on" too --- introducing some
charge sharing effects into the simulation.
This final array holds the pattern of strips that were "on" or "off" ---
no analog information is used in the analysis of the events. The
array was then used as input to
algorithms to find the vertex,
of Si here) was
assumed. A noise level, which was varied from 0.1% to 0.01%
was included in the efficiency function --- this means that a strip which was
not hit has a small probability (Pnoise) to be "on".
If a strip was "on" then each of the adjacent strips were
assumed to have a 10% probability to be "on" too --- introducing some
charge sharing effects into the simulation.
This final array holds the pattern of strips that were "on" or "off" ---
no analog information is used in the analysis of the events. The
array was then used as input to
algorithms to find the vertex, 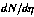 , and
the multiplicity.
, and
the multiplicity.
The inner barrel has a "radius" of R1 = 6.1cm, constrained by
the beam pipe radius of 5 cm. If  is to be measured out to
is to be measured out to 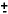 3, the length of the
detector must be
3, the length of the
detector must be 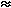 R1/tan(6
R1/tan(6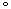 ) =
) = 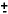 58cm. A length of 50
cm has been chosen. The variation in the vertex position means that for some
events the coverage will extend above (below)
58cm. A length of 50
cm has been chosen. The variation in the vertex position means that for some
events the coverage will extend above (below)  = 3 in the forward
direction with a compensating decrease (increase) in the coverage around
= 3 in the forward
direction with a compensating decrease (increase) in the coverage around
 = -3.
The "radius" of the outer barrel is R2 = 1.5 x R1 = 9.2cm.
= -3.
The "radius" of the outer barrel is R2 = 1.5 x R1 = 9.2cm.
In the following sections some discussion of the loss in performance
expected from a modified
design has been included along with the discussion of the detector
described above. In these discussions, the conceptual design
described here is compared to the vertex detector described in
the Tales/Sparhc Letter of Intent7, which covers only 1/3 of the
azimuthal angle with strips perpendicular to the beam and is 64cm long
instead of 100cm.



Next: The problem of
Up: The Vertex Detector For
Previous: Introduction and Design
Converted to HTML by:
Christine Jarmer
Mon Jun 24 08:52:44 MDT 1996
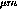 thick silicon
strips with 100
thick silicon
strips with 100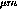 pitch2. Fig. 1 shows schematic views. Half of the
strips in each barrel are oriented parallel to z (the beam direction) and half
orthogonal to z. The parallel and perpendicular strips are sometimes called
"r-
pitch2. Fig. 1 shows schematic views. Half of the
strips in each barrel are oriented parallel to z (the beam direction) and half
orthogonal to z. The parallel and perpendicular strips are sometimes called
"r- 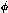 " and "z" strips, respectively.
" and "z" strips, respectively.

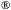 foam
foam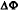 .
.

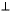
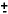 50cm of the center of the vertex detector.
The Gaussian distributions assumed
50cm of the center of the vertex detector.
The Gaussian distributions assumed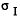 =20, 16, and 5.7cm, for
Au+Au, p+Au, and p+p collisions, respectively.
=20, 16, and 5.7cm, for
Au+Au, p+Au, and p+p collisions, respectively.

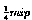 (or 75
(or 75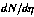 , and
the multiplicity.
, and
the multiplicity.
 is to be measured out to
is to be measured out to 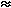 R1/tan(6
R1/tan(6 ) =
) =