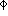 , and z since the Muon Arm is intended to
measure the following characteristics of the detected particle,
, and z since the Muon Arm is intended to
measure the following characteristics of the detected particle,
David M. Lee
Los Alamos National Laboratory, Los Alamos, NM 87545
(submitted: 4 May 1995; revised: 15 May 1995)
The relevant coordinate system for the muon arm is r, 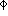 , and z since the Muon Arm is intended to
measure the following characteristics of the detected particle,
, and z since the Muon Arm is intended to
measure the following characteristics of the detected particle,
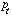 | transverse momentum by measuring the bend in the 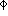 as a function of z; as a function of z; |
 | polar angle by measuring the radial coordinate, r, as a function of z; |
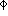 | azimuthal angle. |
However,
the specifications of the LCS will generally be given in terms of the chamber
measurement parameters, position along the anode wires ( high resolution and
approximately 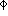 ) and anode wire
position (coarse resolution and approximately r). The Monte Carlo simulations
take these parameters as the input and determine the expected performance of
the muon arm for various physics parameters, i.e., mass resolution of the
upsilon. A position resolution along the anode wires of 100 microns is
desired. This corresponds to all contributions including the intrinsic chamber
resolution and all mechanical construction and alignment uncertainties.
Position resolutions in r of 0.5 cm and in z of 1mm are needed. The
contributions to the resolutions in either r or
) and anode wire
position (coarse resolution and approximately r). The Monte Carlo simulations
take these parameters as the input and determine the expected performance of
the muon arm for various physics parameters, i.e., mass resolution of the
upsilon. A position resolution along the anode wires of 100 microns is
desired. This corresponds to all contributions including the intrinsic chamber
resolution and all mechanical construction and alignment uncertainties.
Position resolutions in r of 0.5 cm and in z of 1mm are needed. The
contributions to the resolutions in either r or 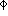 can be tabulated as follows.
can be tabulated as follows.
 | intrinsic chamber resolution |
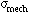 | accuracy for mechanical assembly of the individual planes. |
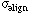 | alignment accuracy from station to station |
 | stability of each station |
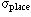 | initial placement accuracy of the octants |
The
Monte Carlo position resolution, 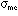 , is
then
, is
then
in phi
and
in r.
and
in z.
The equation for phi implies that the intrinsic resolution of the chambers must be less than 100 um or that the contribution from alignment and construction errors will increase the resolution of the space point of beyond the intrinsic resolution of the chamber.
| azimuthal angle accuracy of the octant assemblies |  = =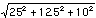 | 29.7 um |
| radial accuracy of the octant assemblies |  | 200 um |
| z accuracy of the octant assemblies |  | 200 um |
Once the octants are assembled we will assume that the assembly is a rigid structure. Alignment fiducials on the space frame carefully surveyed with respect to the alignment pins, will allow the octants to be aligned as a rigid body to the reference points on the magnet.
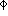 and r and .1mm in z. Cost
will more than likely define what the actual limit is. It is expected that the
alignment precision and the stability for both the r and
and r and .1mm in z. Cost
will more than likely define what the actual limit is. It is expected that the
alignment precision and the stability for both the r and 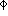 coordinates will be the same. Based on
these numbers the alignment accuracys from station to station will be,
coordinates will be the same. Based on
these numbers the alignment accuracys from station to station will be,
| azimuthal angle accuracy of the station to station alignment |  | 10 um |
| radial accuracy of the station to station alignment | 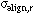 | 10 um |
| azimuthal angle stability of each station |  | 25 um |
| radial stability of each station |  | 25 um. |
| z accuracy from station to station | 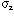 | 0.1 mm. |
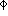 . In conjunction with the initial
placement by optical means the location of the octants will be determined by
the active alignment system. The initial placement precision is,
. In conjunction with the initial
placement by optical means the location of the octants will be determined by
the active alignment system. The initial placement precision is,
| azimuthal angle placement precision | 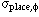 | 10 um |
| radial placement precision | 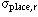 | 10 um |
| z placement precision | 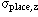 | 10 um |
The initial placement accuracy need only be in the range of the optical and active alignment systems. We expect the placement accuracy to be,
| azimuthal angle placement accuracy | 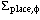 | 5 mm |
| radial placement accuracy | 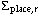 | 5 mm. |
| z placement accuracy | 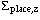 | 5 mm. |
| Error | r | 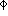 | z | |
|---|---|---|---|---|
 | 0.6 mm | 0.1 mm | ||
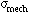 | 0.2 mm | 0.03 mm | 0.2 mm | |
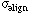 | 0.01 mm | 0.01 mm | ||
 | 0.025 mm | 0.025 mm | 0.1mm | |
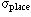 | 0.010 mm | 0.010 mm | 0.010 mm | (precision) |
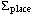 | 5 mm | 5 mm | 5 mm | (accuracy) |
The
error budget for r and z are well within the tolerance required by simulations.
For 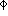 combining the errors we get an
expected space point resolution of 115 um. To achieve a space point resolution
of 100 um, an intrinsic chamber resolution of 82 microns is required.
combining the errors we get an
expected space point resolution of 115 um. To achieve a space point resolution
of 100 um, an intrinsic chamber resolution of 82 microns is required.
The accuracy of the radial coordinate in the global coordinate system (GCS) to the LCS can be determined by the accuracy of the radial measurements in the chambers. The resolution of the radial coordinate in the chambers is 1 cm/sqrt-12 or 2.9 mm. Simulations confirm that a 1 cm anode spacing is adequate for preserving the mass resolution for the upsilon. As a "rule of thumb" we will assume that we want the contributions to errors in any coordinate to be a small fraction due to misalignment and will therefore be one fourth of the measured coordinate. The radial alignment tolerance is then .75 mm.
Multiple scattering in the steel and copper nose cone can be used to find the
alignment tolerances in the azimuthal and polar coordinate as well as the
radial alignment tolerance at station 1 between the LCS and the GCS. The
energy of muons for which we want to determine multiple scattering should be
the highest energy muon. If we assume that these muons originate with the
decay of the 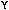 than we will use an upper limit
of 10 GeV. Given this criteria the multiple scattering in the absorber
material is 12 mr and the angular uncertainty on the polar and azimuthal angle
is 7 mr. Projecting this to station 1 yields an uncertainty in r of 13 mm.
To keep the alignment errors in r small when compared to that from multiple
scattering we can use the 1/4 rule and define the alignment tolerance in r to
be 3.3 mm.
than we will use an upper limit
of 10 GeV. Given this criteria the multiple scattering in the absorber
material is 12 mr and the angular uncertainty on the polar and azimuthal angle
is 7 mr. Projecting this to station 1 yields an uncertainty in r of 13 mm.
To keep the alignment errors in r small when compared to that from multiple
scattering we can use the 1/4 rule and define the alignment tolerance in r to
be 3.3 mm.
A 7 mr angular uncertainty on 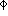 and
and
 will also define the allowable uncertainty the
axis of the muon arm can be away from the beam axis, 1.75 mr from the 1/4 rule.
The length of the muon arm is 4500 mm so that the position of the end of the
muon arm with respect to the front of the muon arm should be known to 31.5 mm
in both x and y and applying the 1/4 rule, 8mm. This implies that we would like
to know the positions of each end of the muon arm magnet 8/sqrt-2 = 5.6 mm. in
each coordinate. Since we don't project back to a x or y coordinate in the
central magnet, the error in angular coordinate of the muon magnet with respect
to the true beam axis is the correct predictor of the allowed errors in the x
and y coordinate. Beam position monitors (BPM) can easily measure the location
of the colliding beams to much better than 5.6 mm. A possible location for
BPM's would be attached to the muon magnet back plate and the support structure
for the chambers at station 1.
will also define the allowable uncertainty the
axis of the muon arm can be away from the beam axis, 1.75 mr from the 1/4 rule.
The length of the muon arm is 4500 mm so that the position of the end of the
muon arm with respect to the front of the muon arm should be known to 31.5 mm
in both x and y and applying the 1/4 rule, 8mm. This implies that we would like
to know the positions of each end of the muon arm magnet 8/sqrt-2 = 5.6 mm. in
each coordinate. Since we don't project back to a x or y coordinate in the
central magnet, the error in angular coordinate of the muon magnet with respect
to the true beam axis is the correct predictor of the allowed errors in the x
and y coordinate. Beam position monitors (BPM) can easily measure the location
of the colliding beams to much better than 5.6 mm. A possible location for
BPM's would be attached to the muon magnet back plate and the support structure
for the chambers at station 1.
The remaining global coordinate is z. Projecting from the spectrometer back through the magnet steel and nose cone to determine the z coordinate will be limited by the multiple scattering angle of 7 mr. Using the multiple scattering error on the projection back to the vertex and using an average angle of 20 degrees to project onto the z axis gives an error in z of 3.7 cm. Simulations have shown that resolutions in z of the position of the vertex of up to 2 cm have no effect on the mass resolution. The alignment tolerance in z will then be one fourth of 2.0 cm or 5 mm.
The Muon Tracker alignment to the beam line and the vertex is,
| alignment tolerance in x an y | 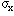 and and 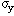 | 3.7 mm |
| alignment tolerance in z | 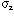 | 5 mm |
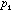 and
and 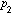 , and the opening
angle,
, and the opening
angle, 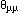 ,
,
The error on the missing mass is,
where
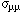 is the error on the opening angle and
is the error on the opening angle and
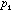 =
= 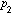 .
.
Assuming the momentum resolution to be 1.8 % then the angle term will dominate
for the smallest opening angle between the North and South Muon Arm, 110
degrees. To keep the error contribution from the angle term small we can apply
the 1/4 rule and equate the angle term to 1/4 of the momentum term and get 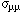 = 13 mr. Since this is the difference between
the two muon angles the allowed tolerance on each of the muon angles is
= 13 mr. Since this is the difference between
the two muon angles the allowed tolerance on each of the muon angles is  _
_ = 13/sqrt-2 = 9.2
mr. Since the 7 mr error that resulted from multiple scattering considerations
is more restrictive, it will be used to define the alignment requirements for
the South Muon Arm. The implication here is that aligning both muon arms to
the beam line and vertex is sufficient to insure good mass resolution.
= 13/sqrt-2 = 9.2
mr. Since the 7 mr error that resulted from multiple scattering considerations
is more restrictive, it will be used to define the alignment requirements for
the South Muon Arm. The implication here is that aligning both muon arms to
the beam line and vertex is sufficient to insure good mass resolution.
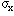 | 3.7 mm |
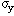 | 3.7 mm |
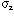 | 5 mm. |
Alignment of Muon Arm to Muon ID
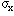 | 3.2 cm |
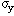 | 3.2 cm |
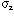 | large |