


Next: Discriminant Analysis
Up: Mu/Pi Discrimination with the
Previous: Data analysis
The algorithms developed for muon identification in PISORP locate hits in
the first plane of the muon identifier and then search for hits in the
second plane. For the results presented here the edges of the pads were
assumed to lie along lines of constant  and
and 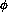 as described in the
PHENIX ``Conceptual Design Report'' (CDR). Therefore the searches were
carried out over prescribed ranges of
as described in the
PHENIX ``Conceptual Design Report'' (CDR). Therefore the searches were
carried out over prescribed ranges of  and
and 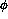 . If any hits are
found in plane 2, the centroid of the hits is calculated and this point
is used as the starting point for a search for hits in plane 3. This
procedure is continued
from plane to plane until plane 6 is reached or until no more hits are
found in the search range.
. If any hits are
found in plane 2, the centroid of the hits is calculated and this point
is used as the starting point for a search for hits in plane 3. This
procedure is continued
from plane to plane until plane 6 is reached or until no more hits are
found in the search range.
In the following we show results for three different track and road-finding
schemes. They are summarized in Fig. 2.
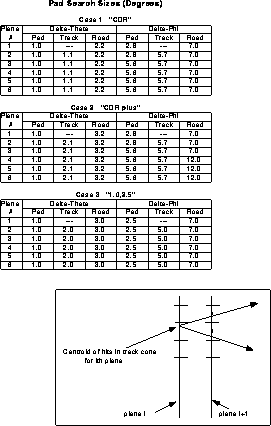
Figure 2: Pad search parameters.
At the top of
the figure the track and road-finding angles are given for the
three cases. Case 1, labeled ``CDR'' uses pad sizes identical to those
specified
in the CDR;
case 2 uses the
same pad sizes but larger search angles than used for case 1;
case 3 uses smaller pads but search angles very similar to case 2.
It is worthwhile, at this point, to comment on the meaning of the
track and road search angles given in the table. For example, for case 1
the track sizes
are designed to search over angular ranges in  of 1.1 degrees and 2.2 degrees in
of 1.1 degrees and 2.2 degrees in 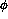 . These numbers were chosen to be
just sufficient
to search over the pad directly behind a pad that registers a
hit in plane 1 (Recall
that a track search is started at every pad that receives
a hit in plane 1)
plus one pad ``below'' and ``above'' in
. These numbers were chosen to be
just sufficient
to search over the pad directly behind a pad that registers a
hit in plane 1 (Recall
that a track search is started at every pad that receives
a hit in plane 1)
plus one pad ``below'' and ``above'' in  and
and 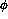 .
Thus, in the second plane, the
search will be made over a rectangular array of
.
Thus, in the second plane, the
search will be made over a rectangular array of
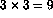 pads. Note that for case 1, the road search angle
pads. Note that for case 1, the road search angle
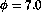 degrees
does not
appear to be large enough to cause the search to extend beyond the
track search range of
degrees
does not
appear to be large enough to cause the search to extend beyond the
track search range of
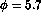 degrees
when going from the first to the second plane. In order to
extend to another pad, the road search angle would need to be greater than
degrees
when going from the first to the second plane. In order to
extend to another pad, the road search angle would need to be greater than
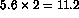 degrees.
However, this is not strictly true because in the
second through
the sixth planes, the centroids of the hits in each plane are
calculated and these centroids
are used as the starting points for the next search.
This means that the hits that are encompassed in the next search
may be different even
if the search
angle is changed by a very small amount. This is illustrated
schematically
at the bottom of Fig. 2 where the search cone, which
starts from plane i just
misses the center of the upper pad in the next plane.
Thus, if one
wishes to translate the search angles to an equivalent number of pads,
one should
keep in mind that this equivalent number of pads is a nominal number.
The number of pads
actually encompassed in each plane depends on the details of
the hit pattern in the preceding plane.
degrees.
However, this is not strictly true because in the
second through
the sixth planes, the centroids of the hits in each plane are
calculated and these centroids
are used as the starting points for the next search.
This means that the hits that are encompassed in the next search
may be different even
if the search
angle is changed by a very small amount. This is illustrated
schematically
at the bottom of Fig. 2 where the search cone, which
starts from plane i just
misses the center of the upper pad in the next plane.
Thus, if one
wishes to translate the search angles to an equivalent number of pads,
one should
keep in mind that this equivalent number of pads is a nominal number.
The number of pads
actually encompassed in each plane depends on the details of
the hit pattern in the preceding plane.



Next: Discriminant Analysis
Up: Mu/Pi Discrimination with the
Previous: Data analysis
Converted to HTML from LaTeX by W. Wayne Kinnison
Thu Aug 24 20:29:25 MDT 1995
 and
and 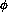 as described in the
PHENIX ``Conceptual Design Report'' (CDR). Therefore the searches were
carried out over prescribed ranges of
as described in the
PHENIX ``Conceptual Design Report'' (CDR). Therefore the searches were
carried out over prescribed ranges of  and
and 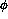 . If any hits are
found in plane 2, the centroid of the hits is calculated and this point
is used as the starting point for a search for hits in plane 3. This
procedure is continued
from plane to plane until plane 6 is reached or until no more hits are
found in the search range.
. If any hits are
found in plane 2, the centroid of the hits is calculated and this point
is used as the starting point for a search for hits in plane 3. This
procedure is continued
from plane to plane until plane 6 is reached or until no more hits are
found in the search range.

 of 1.1 degrees and 2.2 degrees in
of 1.1 degrees and 2.2 degrees in 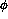 . These numbers were chosen to be
just sufficient
to search over the pad directly behind a pad that registers a
hit in plane 1 (Recall
that a track search is started at every pad that receives
a hit in plane 1)
plus one pad ``below'' and ``above'' in
. These numbers were chosen to be
just sufficient
to search over the pad directly behind a pad that registers a
hit in plane 1 (Recall
that a track search is started at every pad that receives
a hit in plane 1)
plus one pad ``below'' and ``above'' in  and
and 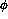 .
Thus, in the second plane, the
search will be made over a rectangular array of
.
Thus, in the second plane, the
search will be made over a rectangular array of
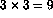 pads. Note that for case 1, the road search angle
pads. Note that for case 1, the road search angle
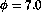 degrees
does not
appear to be large enough to cause the search to extend beyond the
track search range of
degrees
does not
appear to be large enough to cause the search to extend beyond the
track search range of
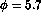 degrees
when going from the first to the second plane. In order to
extend to another pad, the road search angle would need to be greater than
degrees
when going from the first to the second plane. In order to
extend to another pad, the road search angle would need to be greater than
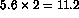 degrees.
However, this is not strictly true because in the
second through
the sixth planes, the centroids of the hits in each plane are
calculated and these centroids
are used as the starting points for the next search.
This means that the hits that are encompassed in the next search
may be different even
if the search
angle is changed by a very small amount. This is illustrated
schematically
at the bottom of Fig.
degrees.
However, this is not strictly true because in the
second through
the sixth planes, the centroids of the hits in each plane are
calculated and these centroids
are used as the starting points for the next search.
This means that the hits that are encompassed in the next search
may be different even
if the search
angle is changed by a very small amount. This is illustrated
schematically
at the bottom of Fig.