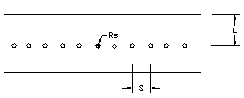
Send Mail to B.V. DineshIn this report, some calculations were carried out to make an estimate of the detector capacitances, assuming a very simple charpak geometry. Additionally, more elaborate calculations taking into account the presence of field wires along with sense wires in the plane are presented.
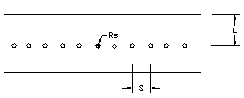
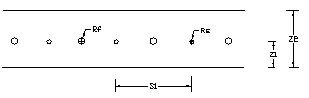
The geometry for the purpose of the calculation is shown in Figure 1. The sense wire plane is sandwiched between two cathode planes, and there are no field shaping wires present in the sense wire plane. The spacing between the sense wire is, `S', the cathode plane to sense wire plane gap `L,' and the radius of the sense wire is Rs.
For the above configuration, the capacitance of the sense wire is given by (Ref. 1),
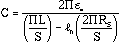.For the PHENIX cathode strip readout chambers, L = 3.175 mm, S = 10 mm, Rs = 0.01 mm. The capacitance for such a chamber turned out to be Cs = 9.16 Pf/meter.
For a cylindrical chamber, the capacitance of the sense wire is given by (Ref. 1),
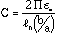.Where `b' is the radius of outer cylinder radius (cathode), and `a' the radius of the sense wire. The capacitance of the sense wire for a = 0.01 mm and b = 3.175 mm would be 9.65 Pf/meter.
The disadvantage of the above two methods of calculation is that one does not take into account the presence of field wires in the sense wire plane. The presence of field wires in the sense wire plane alters the field configuration in such a way that each sense wire behaves like an independent chamber. Thus, the charges induced on cathodes due to the avalanche produced on the anode would be different, as the induced charges are now shared by neighbouring field wires also. A thorough treatment of the calculation of the capacitance must take into account the presence of field wires.
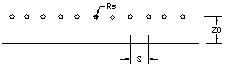
Consider an ideal wire plane parallel to a conducting plane as shown in Figure 2. When such a grid is raised to a potential, the wire plane is charged. As the total charge has to be conserved, there is induction of charge (of opposite polarity) around the wire plane, and also on the conducting plane. As a result, one has a field around the wire plane.
At a distance from grid comparable to or larger than the pitch of the wire plane (S), the potential assumes the value,
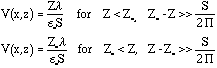
where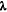 
is the linear charge density along the wire, `S' is the spacing between the wire and Z0 is the distance between the conducting plane to the wire plane. The potential of the wire is given by,
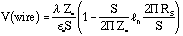
where RS is the radius of the wire. Additional terms arise in the above equation if one has field wires in the same wire plane or due to the presence of anyother high voltage plane. This additional term arises due to the potential induced by the field wire (or high voltage plane) on the sense wires. For a detailed discussion and calculation, refer to Ref. 2.
The geometry of the PHENIX CSC is shown in Figure 3.
As the geometry in a PHENX CSC chamber satisfies the condition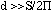 
, one can make use of
the results obtained earlier for the potentials. The potentials, VS, VF, and VC, correspond to the potentials of the sense wire, field wire and cathode plane respectively. Each of them would have 3 terms, one corresponding to the potential of itself, and the other two terms due to the potential induced by the other two planes. The potentials VS, VF, and VC are,
.
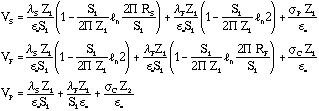In writing the above equations we have assumed that sense wire, field wire, and cathode are all at different potential with respect to the ground plane. However, at a later stage one can set the boundary condition on the voltage to that of PHENIX CSCs. The terms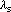 
and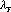 
refer to the linear charge density of the sense and field wires respectively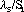, and 
and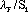 
may be written as 
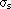and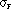 
, the surface charge density of the sense and field wire. 
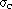is the surface charge density of the cathode plane.
Then the potentials VS, VF, and VC can be represented by matrix,
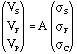
where A is the potential coefficient matrix given by,
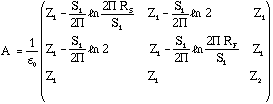.The solution for charges on the different plane is
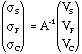.In comparison with elementry physics equation Q=CV, one can identify that matrix A-1 is nothing but capacitance matrix.
For the PHENIX geometry Z1 = 3.175 mm, S1 = 10 mm, RS = 0.01 mm, RF = 0.05 mm, Z2 = 6.35 mm.
Substituting the geometrical dimension of PHENIX CSC in matrix A and inverting it, one obtains
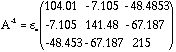.(Note: The capacitance matrix element has the unit, capacitance per unit area.)
The capacitance of the sense wire is Cs = 9.204 pF/meter.
To calculate the induced charges on cathode and field wire, the biasing condition for PHENIX CSC is that VS=V and VF=VC=0. With this condition, one can see that only the terms in the first column of A-1 alone survives for 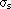, , 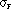and 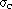respectively. The negative sign for 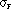and 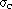indicate that the induced charge has the opposite polarity of the sense wire charges. The charge induced on cathode and field wire by sense wire is in the ratio 
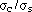and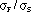 
. The calculated values for 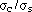and 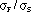for PHENIX CSC are 46.5% and 6.8% respectively.
,
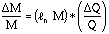where Q=CV and 
Q=C*V + C*V.
Thus, for a stable high voltage, V=0 and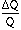 
is due to change in capacitance alone and 
.
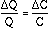In order to find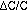 
, one can recalculate the capacitance, with new Z1 and Z2 to take in to account the variation in gap due to the flatness
of the cathode plane. Assuming a variation of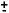 
5 mil in flatness,
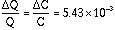.For a detector operating at a gain of M~106
.
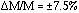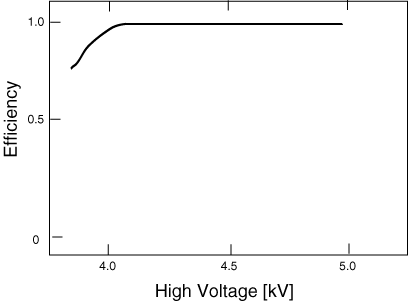
Typically, the plateau extends over few hundred volts. However, in a detector similar to the PHENIX CSCs, where all sense wires are at the same high voltage, because of the flatness variation on the cathode plane, a part of detector may be in a fully efficient operating region whereas elsewhere it may be less efficient. In order to attain full efficiency, it may not be possible to increase the high voltage further as the other region may breakdown. The net effect is that the plateau is shortened by the flatness of the cathode plane.