J.M. Moss
Los Alamos National Laboratory, Los Alamos, NM 87545
(phenix-muon-95-7; submitted 27 April 1995)
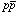 collisions). The event multiplicity was
taken to be 14 charged pions/(pp event). These can be scaled to yield
results for ersatz AuAu collisions at the double HIJET value of 10^4/collision.
The UA1 events were run with a high threshold, 2 GeV and 4 GeV, in order to be
able to throw several million events before I retire. Pat McGaughey is
currently investigating background and multiplicity issues with a complementary
low-threshold configuration.
collisions). The event multiplicity was
taken to be 14 charged pions/(pp event). These can be scaled to yield
results for ersatz AuAu collisions at the double HIJET value of 10^4/collision.
The UA1 events were run with a high threshold, 2 GeV and 4 GeV, in order to be
able to throw several million events before I retire. Pat McGaughey is
currently investigating background and multiplicity issues with a complementary
low-threshold configuration.

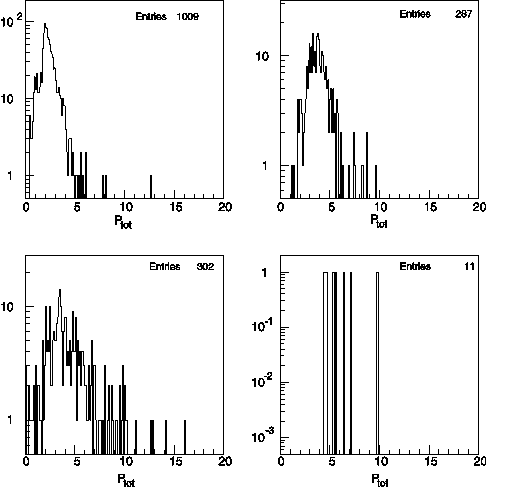
Figure 1: Muons from pion decay reaching station 3 of the muon identifier, top left; non-showering pions which create a signal in plane 3 of the muon identifier, bottom left; Muons from pion decay reaching station 6 of the muon identifier, top right; nonshowering pions which create a signal in plane 6 of the muon identifier, bottom right.
Pair mass spectra are readily created from the singles spectra by event mixing
with an assumed operating luminosity. We take this to be the enhanced
luminosity of polarized pp collision (RSC proposal value), L = 8
x 10^31 cm^-2 sec^-1. This corresponds to a pp collision rate of
r_pp=3.2 x 10^6/sec. The random rate is then F = N_iN_j , where i, j =
, where i, j = 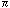 , u and
, u and  = 110 ns.
= 110 ns.
The singles rates from Fig. 1 (left panel) provide a good indication of the level one trigger rates from single pions and muons. To penetrate to muID plane 3 particles require ~ 2 GeV. The ~ 1300 events of Fig. 2 (left panels) translates to ~ 2000 /sec at L = 8 x 10^38 cm^-2, or 2 x 10^-4 per bunch crossing.
The rate of DY events is easily calculated and run through PISA with the same
ntuple analysis as for the random events. Our calculations used the leading
order DY equation with a K-factor of 2 and the Duke S1.1 (leading order)
structure functions from the CERN PDF library. This gives excellent agreement
with the newly published absolute cross sections for DY production at
sqrt-s = 38.7 GeV from E772. The integrated cross section for  > 2 (4) GeV at sqrt-s = 200 GeV
is 6.5 (1.5) nb, giving agreement with Table 3.3 of the PHENIX CDR. Figure 2
displays the results in terms of the absolute number of events recorded with an
integrated luminosity of 8 x 10^38 cm^-2 (10^7 sec of running time). For
simplicity of display, the random spectrum from a muon and a pion in
coincidence has been omitted.
> 2 (4) GeV at sqrt-s = 200 GeV
is 6.5 (1.5) nb, giving agreement with Table 3.3 of the PHENIX CDR. Figure 2
displays the results in terms of the absolute number of events recorded with an
integrated luminosity of 8 x 10^38 cm^-2 (10^7 sec of running time). For
simplicity of display, the random spectrum from a muon and a pion in
coincidence has been omitted.
It is clear, even at the assumed very high luminosity, that there is no serious competition to the DY rate from pion or decay backgrounds. Further, comparison of the the two panels of Fig. 2 shows that most of the pions have showered by the time plane 6 is reached. Thus the requirement of a hit in plane 6 is sufficient to guarantee dominance of the background by decay muons.
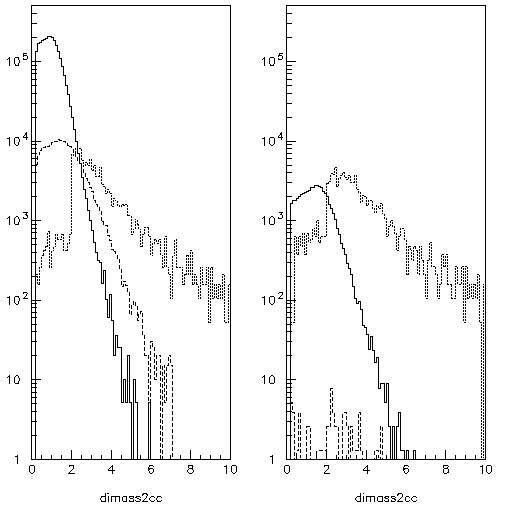
Figure 2: Mass spectra from random coincidences of muons from pion decays and nonshower-ing pions compared to Drell Yan events. The left frame spectra are generated with the requirement of a signal in muID plane 3, while at the right the requirement is muID plane 6. The solid, dashed, and dotted lines are respectively, random muons, random pions, and DY events.
Figure 3 shows that there is no loss in efficiency for DY masses greater than 3.5 GeV from the requirement that the muons penetrate to the back of the identifier. Recall that our muon identification algorithm is the simplest of all imaginable --- penetration to plane x.
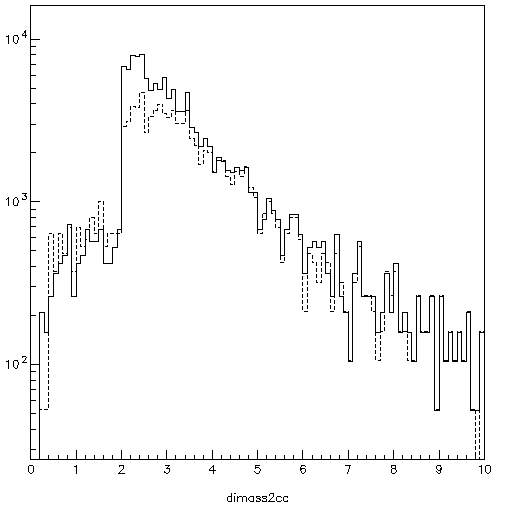
Figure 3: Comparison of DY spectra requiring signals in the 3rd (solid) and 6th (dashed) muID planes.
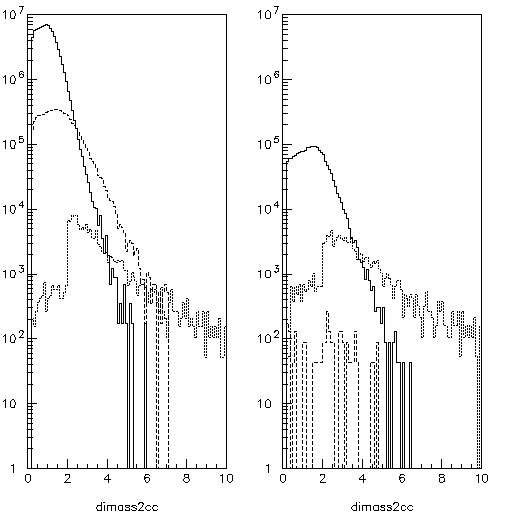
Figure 4: Same as Fig. 2 but with random coincidences scaled for central AuAu collisions.
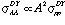 . Happily the PHENIX/CDR luminosity of
AuAu collisions, 2 x 10^27 gives 7.7 x 10^31 cm^-2 sec^-1 for DY events, thus
requiring no correction for comparison to pp. Soft particle production
in central collisions scales as
. Happily the PHENIX/CDR luminosity of
AuAu collisions, 2 x 10^27 gives 7.7 x 10^31 cm^-2 sec^-1 for DY events, thus
requiring no correction for comparison to pp. Soft particle production
in central collisions scales as 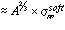 . While
pions in the region p > 2 GeV may have a nuclear dependence closer to
unity, we will assume 2/3 for the present case. This gives
. While
pions in the region p > 2 GeV may have a nuclear dependence closer to
unity, we will assume 2/3 for the present case. This gives 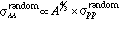 , so that the signal-background gets worse
by
, so that the signal-background gets worse
by 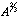 with respect to DY. Figure 4 shows the
spectra of Fig. 2 with the random backgrounds multiplied by
with respect to DY. Figure 4 shows the
spectra of Fig. 2 with the random backgrounds multiplied by 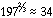 . This is a somewhat more optimistic signal to background
than Fig. 3.6 of the PHENIX-CDR where the decay and DY signals are shown
crossing at about 5 GeV.
. This is a somewhat more optimistic signal to background
than Fig. 3.6 of the PHENIX-CDR where the decay and DY signals are shown
crossing at about 5 GeV.
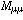 = 4 GeV from random pions or random muons
from pion decay,[1]
= 4 GeV from random pions or random muons
from pion decay,[1]
Before the above statements are taken as gospel, high threshold PISA runs must be combined with the typical multiplicity distributions from very low threshold runs. Additionally, one needs to look into the background from beam gas interactions. My guess is that these further refinements won't change the outcome much. They will, however, allow one to define the required channel count in the muID for the south arm.
I would like to add a few more items to the list which require further scrutiny for the south arm muID system. These are:
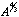 , does one need pad readout?
, does one need pad readout?
 road
finding of the PHENIX/CDR-Update be replaced with an x-y scheme?
road
finding of the PHENIX/CDR-Update be replaced with an x-y scheme?
These are some of the issues which need to be on the table if we are to make intelligent use of the funds for the spin upgrade.